5章数式環境

著者:梅谷武

作成:2013-09-15
更新:2013-09-19

equation環境は数式番号を付けるための環境である。'*'を後置することにより、数式番号を付けない事もできる。数式番号は一つのファイル内で一意的に定まる初期値(既定値は1)から始まる通し番号である。数式番号の初期値はプリアンブルで次のように設定することができる。

¥setcounter{equation}{<数値>}

プリアンブルで章番号を指定した場合、

"数式番号" = "章番号" + '.' + "数式番号"

と置き換えられる。数式番号には"eqn"+"数式番号"というアンカーが埋め込まれる。

¥begin{equation}
S = ¥sqrt{s(s - a)(s - b)(s - c)}
¥end{equation}

(5.1)

S = √s(s - a)(s - b)(s - c)

¥begin{equation*}
S = ¥sqrt{s(s - a)(s - b)(s - c)}
¥end{equation*}

S = √s(s - a)(s - b)(s - c)

¥begin{equation}
a_1 X_1 + ¥cdots + a_n X_n ¥equiv b (¥mod m)
¥end{equation}

(5.2)

a₁ X₁ + ⋯ + a_n X_n ≡ b (mod m)

¥begin{equation*}
a_1 X_1 + ¥cdots + a_n X_n ¥equiv b (¥mod m)
¥end{equation*}

a₁ X₁ + ⋯ + a_n X_n ≡ b (mod m)

5.2 eqnarray環境

eqnarray環境は複数行の数式を縦方向に揃えてレイアウトする。一行の数式は、

左辺ブロック
関係子
右辺ブロック

の三つのブロックから成る。ブロックとは{}で囲まれたテーブルモード数式である。これを続けることで任意の行数の数式を表現することができる。行間は"¥¥"で検出する。関係子は記号や記号列からなるブロックで、これを基準にして数式を縦に揃える。数式番号は左辺ブロックが空でない行に付けられる。'*'を後置することにより、数式番号を付けない事もできる。

¥begin{eqnarray}
{F^{-1}・F(f)(ζ^r)}=
{n^{-1}¥sum_{t=0}^{n-1}{F(f)(ζ^t)ζ^{-tr}}}¥¥
{}={n^{-1}¥sum_{t=0}^{n-1}{(¥sum_{s=0}^{n-1}{f(ζ^s)ζ^{st}})ζ^{-tr}}}¥¥
{}={n^{-1}¥sum_{s=0}^{n-1}{f(ζ^s)(¥sum_{t=0}^{n-1}{ζ^{t(s-r)}})}}¥¥
{}={n^{-1}f(ζ^r)(¥sum_{t=0}^{n-1}{ζ^0)}}¥¥
{}={f(ζ^r)}
¥end{eqnarray}

(5.3)

F^-1・F(f)(ζ^r)

n^-1

n-1
∑
t=0

F(f)(ζ^t)ζ^-tr

n^-1

n-1
∑
t=0

(

n-1
∑
s=0

f(ζ^s)ζ^st

)ζ^-tr

n^-1

n-1
∑
s=0

f(ζ^s)(

n-1
∑
t=0

ζ^t(s-r)

)

n^-1f(ζ^r)(

n-1
∑
t=0

ζ⁰)

f(ζ^r)

¥begin{eqnarray*}
{F^{-1}・F(f)(ζ^r)}=
{n^{-1}¥sum_{t=0}^{n-1}{F(f)(ζ^t)ζ^{-tr}}}¥¥
{}={n^{-1}¥sum_{t=0}^{n-1}{(¥sum_{s=0}^{n-1}{f(ζ^s)ζ^{st}})ζ^{-tr}}}¥¥
{}={n^{-1}¥sum_{s=0}^{n-1}{f(ζ^s)(¥sum_{t=0}^{n-1}{ζ^{t(s-r)}})}}¥¥
{}={n^{-1}f(ζ^r)(¥sum_{t=0}^{n-1}{ζ^0)}}¥¥
{}={f(ζ^r)}
¥end{eqnarray*}

F^-1・F(f)(ζ^r)

n^-1

n-1
∑
t=0

F(f)(ζ^t)ζ^-tr

n^-1

n-1
∑
t=0

(

n-1
∑
s=0

f(ζ^s)ζ^st

)ζ^-tr

n^-1

n-1
∑
s=0

f(ζ^s)(

n-1
∑
t=0

ζ^t(s-r)

)

n^-1f(ζ^r)(

n-1
∑
t=0

ζ⁰)

f(ζ^r)

5.3 mathlist環境

mathlist環境は数式を含む項目を箇条書きするときに使う。使い方はdescripition環境と同じである。項目の内容は自動的にテーブルモード数式変換される。

¥begin{mathlist}[20]
¥item[(結合律)] 任意のa,b,cについて、(ab)c = a(bc)
¥item[(単位元)] 1と任意のaについて、a1 = 1a = a
¥item[(可換律)] 任意のa,bについて、ab = ba
¥item[(分配律)] 任意のa,b,cについて、
¥array_{¥lc48}{ a(b~+~c)~=~ab~+~ac ;  (a~+~b)c~=~ac~+~bc ;}
¥end{mathlist}

(結合律)

任意のa,b,cについて、(ab)c = a(bc)

(単位元)

1と任意のaについて、a1 = 1a = a

(可換律)

任意のa,bについて、ab = ba

(分配律)

任意のa,b,cについて、

a(b + c) = ab + ac

(a + b)c = ac + bc

5.4 定理環境

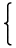定理環境は属性付き段落として実装されており、利用者が表示用識別子を定義することができる。識別子を明示的に指定しないときには段落番号が識別子として使われる。定理環境の題名には'a'+段落番号がアンカーとして埋め込まれる。

¥theorem{属性名:別名[:利用者定義識別子]}

証明には¥proof命令を使う。

¥theorem{定理:秦九韶の大衍求一術の原理:I}
$m_1,m_2,\cdots,m_k$を任意の正の整数としたときに、連立一次合同式
¥[
¥array_{¥lc144}{
  X~¥equiv~a_1~(¥mod~m_1);
  X~¥equiv~a_2~(¥mod~m_2);
  \vdots;
  X~¥equiv~a_k~(¥mod~m_k);
}
¥]
は
¥[
a_i ¥equiv a_j (¥mod gcd(m_i,m_j)), 1 ¥leqq i, j ¥leqq k, i ¥neq j
¥]
が成り立つときに$m_1,m_2,\cdots,m_k$の最小公倍数を法として一意的な解を持つ。
↵
¥proof{証明}
演習とする。

定理I 秦九韶の大衍求一術の原理

m₁,m₂,⋯,m_kを任意の正の整数としたときに、連立一次合同式

X ≡ a₁ (mod m₁)

X ≡ a₂ (mod m₂)

⋮

X ≡ a_k (mod m_k)

は

a_i ≡ a_j (mod gcd(m_i,m_j)), 1 ≦ i, j ≦ k, i ≠ j

が成り立つときにm₁,m₂,⋯,m_kの最小公倍数を法として一意的な解を持つ。

証明

演習とする。■

梅谷武『ktexマニュアル』はクリエイティブ・コモンズ表示 3.0 非移植ライセンスで利用できます。