FormedTextにおける数式記述

著者:梅谷武
語句:TeX

FormedTextにおける数式記述の書式について定める。

作成:2006-02-27
更新:2011-03-10

TeXにおいては複雑な数式がテキストとして簡単に入力できるように工夫されています。FormedTextでは、このTeXにおける数式記述方法をHTMLで実装できる程度に縮小し、さらに一部の命令をUNICODE(UTF-8)符号で置き換えられるようにしています。

FormedTextには次の５種類の数式タグがあります。

qt → 本文内に数式を埋め込む(TeXのテキスト用数式モード'$'に対応)
qd → 本文とは別に表示領域を確保する(ディスプレイ用数式モード '\['に対応)
qdarray → 複数行の数式をそろえて表示する(eqnarray*環境に対応)
eqn → qdに数式番号を付ける(equation環境に対応)
eqnarray → qdarrayに数式番号を付ける(eqnarray環境に対応)

TeX

TeXはD.E.Knuthが "The Art of Computer Programming"の組版のために開発した数式を美しく描くことができる組版システムです。オープンソースのフリーソフトウェアとして公開されていて、研究者が論文を書くツールとして広く普及しているだけでなく、商業出版にも使われています。

2 qt:テキスト用数式タグ

2.1 概要

XML構文の制約から半角の不等号の代わりに全角の不等号を使います。つまり、<の代わりに＜を、>の代わりに＞を使用します。&は数式タグ中では使用できません。

2.2 _:下付き命令

<qt>x_i, x_下, x_{i+1}</qt>

x_i, x_下, x_i+1

2.3 ^:上付き命令

<qt>x^i, x^上, x^{i+1}</qt>

xⁱ, x^上, xⁱ⁺¹

2.4 `:太字命令

TeXにおける\mathbf命令に対応しています。

<qt>R^n, \bm{R}^n, \bm{R^n}, \bm{実}数</qt>

Rⁿ, Rⁿ, Rⁿ, 実数

2.5 √, ∛, ∜:根号

平方根、立方根、4乗根が表現できます。√は\sqrtで置き換えることができます。

<qt>√2, √{x^2 + y^2}, √{x_0 + y_0}, ∛2, ∜2</qt>

√2, √x² + y², √x₀ + y₀, ∛2, ∜2

2.6 \:制御文字

"\"はTeXと同様に制御文字として機能します。他の数式タグにおいてはこれに命令文字列を続けて命令として働かせることができますが、qtタグにおいてはsqrt, underline, overline, det, normと関数名だけが有効です。

<qt>\ , \{, \}, \%, \$, \# \\
\sin(x) ＜ y, y ＞ \log(x)</qt>

, {, }, %, $, \#
sin(x) ＜ y, y ＞ log(x)

<qt>\sqrt{x + y}, \underline{x + y}, \overline{x + y}}, \det{a}, \norm{`A}</qt>

√x + y, x + y, x + y, a, `A

2.7 ~:空白指定

数式タグにおいて" "はTeXと同様に明示的な空白指定として機能します。HTML形式においては半角スペースに置き換わり、" "は全角スペースに置き換わります。

<qt>a~b　cdef</qt>

a b cdef

3 qd:ディスプレイ用数式タグ

3.1 命令｛引数文字列｝

根号

√, ∛, ∜によって平方根、立方根、4乗根が表現できます。√は\sqrtで置き換えることができます。テキスト用です。

<qd>\sqrt{2}, √{2}, ∛2, ∜2</qd>

√2, √2, ∛2, ∜2

¥underline, ¥overline

\underlineは下線を、øverlineは上線を引きます。テキスト用です。

<qd>\underline{x + y}, \overline{x + y}</qd>

x + y, x + y

¥det, ¥norm

\detは絶対値あるいは行列式、\normはノルムを表わします。

<qd>\det{\frac{1}{\sum_{i=0}^{n}{x^i}} \ \norm{\frac{df}{dx}}</qd>

n
∑
i=0

xⁱ

3.2 命令＿｛引数文字列｝＾｛引数文字列｝｛引数文字列｝

¥sum, ¥prod

∑は∑(#x2211)、∏は∏(#x220f)で置き換えることができます。これはギリシャ大文字のΣ、Πとは異なります。

<qd>\sum_{i=0}^{n}{x^i} \ \prod_{i=0}^{n}{x^i}</qd>

n
∑
i=0

xⁱ

n
∏
i=0

xⁱ

¥bigcap, ¥bigcup

<qd>\bigcap_{i=0}^{n}{S_i} \ \bigcup_{i=0}^{n}{T_i}</qd>

n
∩
i=0

S_i

n
∪
i=0

T_i

¥sup, ¥inf, ¥max, ¥min, ¥lim, ¥limsup, ¥liminf

<qd>\inf_{i=0,…,n}{x_i} \ \lim_{i→∞}{x_i}</qd>

inf
i=0,…,n

x_i

lim
i→∞

x_i

¥int, ¥int2, ¥int3, ¥oint

¥intは∫(#x222b)、¥int2は∬(#x222c)、¥int3は∭(#x222d)、¥ointは∮(#x222e)で置き換えることができます。

<qd>∫_0^1{f(x)dx} \ ∬_D{f(x,y)dxdy}
\ ∭_V{f(x,y,z)dxdydz} \ ∮_C{f(x,y)dC}</qd>

∫

1

0

f(x)dx

∬

f(x,y)dxdy

∭

f(x,y,z)dxdydz

∮

f(x,y)dC

3.3 命令｛引数文字列1｝｛引数文字列2｝

¥frac

\fracは分数を表現する命令です。

<qd>\frac{1}{\sum_{i=0}^{n}{x^i} \ \frac{df}{dx}</qd>

n
∑
i=0

xⁱ

<qd>\frac{c_1}{b_1 + \frac{c_2}{b_2 + \frac{c_3}{b_3}}}</qd>

c₁

b₁ +

c₂

b₂ +

c₃

b₃

\binom,

\stir1, \stir2, \gauss, \jacobi

¥binomは２項係数、¥stir1は第１種スターリング数、¥stir2は第２種スターリング数、¥gaussはガウス記号、¥jacobiは平方剰余記号を表現します。

<qd>\binom{n}{k} \ \stir1{n}{k} \ \stir2{n}{k}
\ \gauss{n}{k} \ \jacobi{n}{k}</qd>

(

n
k

)

[

n
k

]

{

n
k

}

[

n
k

]

(

n
k

)

3.4 ¥array＿｛左括弧｝＾｛右括弧｝｛引数文字列｝

¥array命令で行列を表現します。引数文字列においては ';'で行間区切りを、スペースで項目区切りを表わします。列の揃え方は中央揃えですが、この命令の後にc,l,rという文字を付け加えることによって(¥arrayc, ¥arrayl, ¥arrayr)、列の揃え方を指定することができます。引数の_命令で左括弧文字を、^命令で右括弧文字を指定できます。

<qd>\array_{\lb96}^{\rb96}{
a_{11} … a_{1n} ;
： ： ： ;
a_{m1} … a_{mn} ;
}
\det{\array{
a_{11} … a_{1n} ;
： ： ： ;
a_{m1} … a_{mn} ;
}}
</qd>

a₁₁

…

a_1n

：

a_m1

…

a_mn

a₁₁

…

a_1n

：

a_m1

…

a_mn

<qd>\array_{\lb192}^{\lb192}{
\frac{∂g_1}{∂x_1} … \frac{∂g_1}{∂x_n} ;
： ： ： ;
\frac{∂g_n}{∂x_1} … \frac{∂g_n}{∂x_n} ;
}
\det{\array{
\frac{∂g_1}{∂x_1} … \frac{∂g_1}{∂x_n} ;
： ： ： ;
\frac{∂g_n}{∂x_1} … \frac{∂g_n}{∂x_n} ;
}}
</qd>

∂g₁

∂x₁

…

∂g₁

∂x_n

：

∂g_n

∂x₁

…

∂g_n

∂x_n

∂g₁

∂x₁

…

∂g₁

∂x_n

：

∂g_n

∂x₁

…

∂g_n

∂x_n

<qd>
δ_{ij} = \array_{\lc48}{
0, i≠j;
1, i=j;
}
</qd>

δ_ij =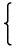

i≠j

i=j

3.5 ¥up｛引数文字列｝

\up命令は行列の添え字のための命令です。

<qd>\up{t}\array_{\lb96}^{\rb96}{
a b c ;
d e f ;
g h i ;
}\up{-1} = 
\array_{\lb96}^{\rb96}{
A B C ;
D E F ;
G H I ;
}
</qd>

-1

3.6 関数名

¥sin, ¥cos, ¥tan, ¥sec, ¥csc, ¥cot, ¥sinh, ¥cosh, ¥tanh, ¥coth, ¥arcsin, ¥arccos, ¥arctan, ¥exp, ¥log, ¥mod, ¥max, ¥min

<qd>\sin x,\ \sin(x+y),\ 3≡1(\mod~2)</qd>

sin x, sin(x+y), 3≡1(mod 2)

3.7 画像フォント

¥longrightarrow, ¥longmapsto

<qd>`R \longrightarrow `C, i \longmapsto `z</qd>

`C, i

¥lb???, ¥rb???, ¥lc???, ¥rc???

先頭の英文字列はフォント名、続く数字はフォントの高さ[ピクセル]を表わします。

<qd>\lb36 \rb36 \lb48 \rb48 \lb72 \rb72
\lb96 \rb96 \lb144 \rb144 \lb192 \rb192 \lb288 \rb288</qd>

<qd>\lc36 \rc36 \lc48 \rc48 \lc72 \rc72
\lc96 \rc96 \lc144 \rc144 \lc192 \rc192 \lc288 \rc288</qd>

4 qdarray:複数行数式タグ

qdarrayタグは複数行の数式を縦方向に揃えてレイアウトします。一行の数式は、

左辺ブロック
関係子
右辺ブロック

の三つのブロックから成ります。ブロックとはで囲まれたqdタグの数式です。これを続けることで任意の行数の数式を表現することができます。行間は改行"\"で検出します。関係子は記号や記号列からなるブロックで、これを基準にして数式を縦に揃えます。

<qdarray>
{F^{-1}・F(f)(ζ^r)} = 
{n^{-1}\sum_{t=0}^{n-1}{F(f)(ζ^t)ζ^{-tr}}} \\
{} = {n^{-1}\sum_{t=0}^{n-1}{(\sum_{s=0}^{n-1}{f(ζ^s)ζ^{st}})ζ^{-tr}}} \\
{} = {n^{-1}\sum_{s=0}^{n-1}{f(ζ^s)(\sum_{t=0}^{n-1}{ζ^{t(s-r)}})}}\\
{} = {n^{-1}f(ζ^r)(\sum_{t=0}^{n-1}{ζ^0)}}\\
{} = f(ζ^r)
</qdarray>

F^-1・F(f)(ζ^r)

n^-1

n-1
∑
t=0

F(f)(ζ^t)ζ^-tr

n^-1

n-1
∑
t=0

(

n-1
∑
s=0

f(ζ^s)ζ^st

)ζ^-tr

n^-1

n-1
∑
s=0

f(ζ^s)(

n-1
∑
t=0

ζ^t(s-r)

)

n^-1f(ζ^r)(

n-1
∑
t=0

ζ⁰)

f(ζ^r)

5 eqn:番号付き数式タグ

eqnタグはqdタグと同機能で、さらに自動的に数式番号が付き、"eqn"+"数式番号"というアンカーが埋め込まれます。

<eqn>S = √{s(s - a)(s - b)(s - c)}</eqn>

(1)

S = √s(s - a)(s - b)(s - c)

6 eqnarray:番号付き複数行数式タグ

eqnarrayタグはqdarrayタグと同機能で、さらに自動的に数式番号が付き、"eqn"+"数式番号"というアンカーが埋め込まれます。数式番号は左辺ブロックがある行にだけ付けられます。

<eqnarray>
{\sin α ＋ \sin β} = {2\sin \frac{α ＋ β}{2} \cos \frac{α － β}{2} } \\
{\sin α － \sin β} = {2\sin \frac{α － β}{2} \cos \frac{α ＋ β}{2} } \\
{\cos α ＋ \cos β} = {2\cos \frac{α ＋ β}{2} \cos \frac{α － β}{2} } \\
{\cos α － \cos β} = {－2\sin \frac{α ＋ β}{2} \sin \frac{α － β}{2} }
</eqnarray>

(2)

sin α ＋ sin β

2sin

α ＋ β

cos

α － β

(3)

sin α － sin β

2sin

α － β

cos

α ＋ β

(4)

cos α ＋ cos β

2cos

α ＋ β

cos

α － β

(5)

cos α － cos β

－2sin

α ＋ β

sin

α － β

<eqnarray>
{F^{-1}・F(f)(ζ^r)} = 
{n^{-1}\sum_{t=0}^{n-1}{F(f)(ζ^t)ζ^{-tr}}} \\
{} = {n^{-1}\sum_{t=0}^{n-1}{(\sum_{s=0}^{n-1}{f(ζ^s)ζ^{st}})ζ^{-tr}}} \\
{} = {n^{-1}\sum_{s=0}^{n-1}{f(ζ^s)(\sum_{t=0}^{n-1}{ζ^{t(s-r)}})}}\\
{} = {n^{-1}f(ζ^r)(\sum_{t=0}^{n-1}{ζ^0)}}\\
{} = f(ζ^r)
</eqnarray>

(6)

F^-1・F(f)(ζ^r)

n^-1

n-1
∑
t=0

F(f)(ζ^t)ζ^-tr

n^-1

n-1
∑
t=0

(

n-1
∑
s=0

f(ζ^s)ζ^st

)ζ^-tr

n^-1

n-1
∑
s=0

f(ζ^s)(

n-1
∑
t=0

ζ^t(s-r)

)

n^-1f(ζ^r)(

n-1
∑
t=0

ζ⁰)

f(ζ^r)

7 qdlist:見出し付き箇条書き(数式用)

箇条書きに自由に見出しを付けたいときに使います。left属性は見出しの長さが全体に占める割合を

<qdlist left='15' align='center'>
(見出し1):\frac{√{s(s - a)(s - b)(s - c)}}{S} = 1
(見出し2):δ_{ij} = \array_{\lc48}{  0, i≠j;  1, i=j; }
</qdlist>

(見出し1)

√s(s - a)(s - b)(s - c)

= 1

(見出し2)

δ_ij =

i≠j

i=j

8 数学記号

8.1 ギリシャ文字

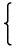alpha	Α	α
beta	Β	β
gamma	Γ	γ
delta	Δ	δ
epsilon	Ε	ε
zeta	Ζ	ζ
eta	Η	η
theta	Θ	θ
iota	Ι	ι
kappa	Κ	κ
lambda	Λ	λ
mu	Μ	μ
nu	Ν	ν
xi	Ξ	ξ
omicron	Ο	ο
pi	Π	π
rho	Ρ	ρ
sigma	Σ	σ
tau	Τ	τ
upsilon	Υ	υ
phi	Φ	φ
chi	Χ	χ
psi	Ψ	ψ
omega	Ω	ω

8.2 ギリシャ異体・拡張文字

epsilon	ℇ
theta	ϑ
pi	ϖ
rho	ϱ
sigma	ς
phi	ϕ
stigma	Ϛ
digamma	Ϝ
sampi	Ϡ
qoppa	Ϟ

8.3 文字様記号(#2100～#2138)

00	01	02	03	04	05	06	07	08	09	0a	0b	0c	0d	0e	0f
℀	℁	ℂ	℃	℄	℅	℆	ℇ	℈	℉	ℊ	ℋ	ℌ	ℍ	ℎ	ℏ
ℐ	ℑ	ℒ	ℓ	℔	ℕ	№	℗	℘	ℙ	ℚ	ℛ	ℜ	ℝ	℞	℟
℠	℡	™	℣	ℤ	℥	Ω	℧	ℨ	℩	K	Å	ℬ	ℭ	℮	ℯ
ℰ	ℱ	Ⅎ	ℳ	ℴ	ℵ	ℶ	ℷ	ℸ

8.4 数字の形(#2153～#2182)

00	01	02	03	04	05	06	07	08	09	0a	0b	0c	0d	0e	0f
			⅓	⅔	⅕	⅖	⅗	⅘	⅙	⅚	⅛	⅜	⅝	⅞	⅟
Ⅰ	Ⅱ	Ⅲ	Ⅳ	Ⅴ	Ⅵ	Ⅶ	Ⅷ	Ⅸ	Ⅹ	Ⅺ	Ⅻ	Ⅼ	Ⅽ	Ⅾ	Ⅿ
ⅰ	ⅱ	ⅲ	ⅳ	ⅴ	ⅵ	ⅶ	ⅷ	ⅸ	ⅹ	ⅺ	ⅻ	ⅼ	ⅽ	ⅾ	ⅿ
ↀ	ↁ	ↂ

8.5 矢印(#2190～#21ea)

00	01	02	03	04	05	06	07	08	09	0a	0b	0c	0d	0e	0f
←	↑	→	↓	↔	↕	↖	↗	↘	↙	↚	↛	↜	↝	↞	↟
↠	↡	↢	↣	↤	↥	↦	↧	↨	↩	↪	↫	↬	↭	↮	↯
↰	↱	↲	↳	↴	↵	↶	↷	↸	↹	↺	↻	↼	↽	↾	↿
⇀	⇁	⇂	⇃	⇄	⇅	⇆	⇇	⇈	⇉	⇊	⇋	⇌	⇍	⇎	⇏
⇐	⇑	⇒	⇓	⇔	⇕	⇖	⇗	⇘	⇙	⇚	⇛	⇜	⇝	⇞	⇟
⇠	⇡	⇢	⇣	⇤	⇥	⇦	⇧	⇨	⇩	⇪

8.6 数学記号(#2200～#22f1)

00	01	02	03	04	05	06	07	08	09	0a	0b	0c	0d	0e	0f
∀	∁	∂	∃	∄	∅	∆	∇	∈	∉	∊	∋	∌	∍	∎	∏
∐	∑	−	∓	∔	∕	∖	∗	∘	∙	√	∛	∜	∝	∞	∟
∠	∡	∢	∣	∤	∥	∦	∧	∨	∩	∪	∫	∬	∭	∮	∯
∰	∱	∲	∳	∴	∵	∶	∷	∸	∹	∺	∻	∼	∽	∾	∿
≀	≁	≂	≃	≄	≅	≆	≇	≈	≉	≊	≋	≌	≍	≎	≏
≐	≑	≒	≓	≔	≕	≖	≗	≘	≙	≚	≛	≜	≝	≞	≟
≠	≡	≢	≣	≤	≥	≦	≧	≨	≩	≪	≫	≬	≭	≮	≯
≰	≱	≲	≳	≴	≵	≶	≷	≸	≹	≺	≻	≼	≽	≾	≿
⊀	⊁	⊂	⊃	⊄	⊅	⊆	⊇	⊈	⊉	⊊	⊋	⊌	⊍	⊎	⊏
⊐	⊑	⊒	⊓	⊔	⊕	⊖	⊗	⊘	⊙	⊚	⊛	⊜	⊝	⊞	⊟
⊠	⊡	⊢	⊣	⊤	⊥	⊦	⊧	⊨	⊩	⊪	⊫	⊬	⊭	⊮	⊯
⊰	⊱	⊲	⊳	⊴	⊵	⊶	⊷	⊸	⊹	⊺	⊻	⊼	⊽	⊾	⊿
⋀	⋁	⋂	⋃	⋄	⋅	⋆	⋇	⋈	⋉	⋊	⋋	⋌	⋍	⋎	⋏
⋐	⋑	⋒	⋓	⋔	⋕	⋖	⋗	⋘	⋙	⋚	⋛	⋜	⋝	⋞	⋟
⋠	⋡	⋢	⋣	⋤	⋥	⋦	⋧	⋨	⋩	⋪	⋫	⋬	⋭	⋮	⋯
⋰	⋱

Published by SANENSYA Co.,Ltd.

00	01	02	03	04	05	06	07	08	09	0a	0b	0c	0d	0e	0f
℀	℁	ℂ	℃	℄	℅	℆	ℇ	℈	℉	ℊ	ℋ	ℌ	ℍ	ℎ	ℏ
ℐ	ℑ	ℒ	ℓ	℔	ℕ	№	℗	℘	ℙ	ℚ	ℛ	ℜ	ℝ	℞	℟
℠	℡	™	℣	ℤ	℥	Ω	℧	ℨ	℩	K	Å	ℬ	ℭ	℮	ℯ
ℰ	ℱ	Ⅎ	ℳ	ℴ	ℵ	ℶ	ℷ	ℸ

00	01	02	03	04	05	06	07	08	09	0a	0b	0c	0d	0e	0f
			⅓	⅔	⅕	⅖	⅗	⅘	⅙	⅚	⅛	⅜	⅝	⅞	⅟
Ⅰ	Ⅱ	Ⅲ	Ⅳ	Ⅴ	Ⅵ	Ⅶ	Ⅷ	Ⅸ	Ⅹ	Ⅺ	Ⅻ	Ⅼ	Ⅽ	Ⅾ	Ⅿ
ⅰ	ⅱ	ⅲ	ⅳ	ⅴ	ⅵ	ⅶ	ⅷ	ⅸ	ⅹ	ⅺ	ⅻ	ⅼ	ⅽ	ⅾ	ⅿ
ↀ	ↁ	ↂ

00	01	02	03	04	05	06	07	08	09	0a	0b	0c	0d	0e	0f
←	↑	→	↓	↔	↕	↖	↗	↘	↙	↚	↛	↜	↝	↞	↟
↠	↡	↢	↣	↤	↥	↦	↧	↨	↩	↪	↫	↬	↭	↮	↯
↰	↱	↲	↳	↴	↵	↶	↷	↸	↹	↺	↻	↼	↽	↾	↿
⇀	⇁	⇂	⇃	⇄	⇅	⇆	⇇	⇈	⇉	⇊	⇋	⇌	⇍	⇎	⇏
⇐	⇑	⇒	⇓	⇔	⇕	⇖	⇗	⇘	⇙	⇚	⇛	⇜	⇝	⇞	⇟
⇠	⇡	⇢	⇣	⇤	⇥	⇦	⇧	⇨	⇩	⇪

00	01	02	03	04	05	06	07	08	09	0a	0b	0c	0d	0e	0f
∀	∁	∂	∃	∄	∅	∆	∇	∈	∉	∊	∋	∌	∍	∎	∏
∐	∑	−	∓	∔	∕	∖	∗	∘	∙	√	∛	∜	∝	∞	∟
∠	∡	∢	∣	∤	∥	∦	∧	∨	∩	∪	∫	∬	∭	∮	∯
∰	∱	∲	∳	∴	∵	∶	∷	∸	∹	∺	∻	∼	∽	∾	∿
≀	≁	≂	≃	≄	≅	≆	≇	≈	≉	≊	≋	≌	≍	≎	≏
≐	≑	≒	≓	≔	≕	≖	≗	≘	≙	≚	≛	≜	≝	≞	≟
≠	≡	≢	≣	≤	≥	≦	≧	≨	≩	≪	≫	≬	≭	≮	≯
≰	≱	≲	≳	≴	≵	≶	≷	≸	≹	≺	≻	≼	≽	≾	≿
⊀	⊁	⊂	⊃	⊄	⊅	⊆	⊇	⊈	⊉	⊊	⊋	⊌	⊍	⊎	⊏
⊐	⊑	⊒	⊓	⊔	⊕	⊖	⊗	⊘	⊙	⊚	⊛	⊜	⊝	⊞	⊟
⊠	⊡	⊢	⊣	⊤	⊥	⊦	⊧	⊨	⊩	⊪	⊫	⊬	⊭	⊮	⊯
⊰	⊱	⊲	⊳	⊴	⊵	⊶	⊷	⊸	⊹	⊺	⊻	⊼	⊽	⊾	⊿
⋀	⋁	⋂	⋃	⋄	⋅	⋆	⋇	⋈	⋉	⋊	⋋	⋌	⋍	⋎	⋏
⋐	⋑	⋒	⋓	⋔	⋕	⋖	⋗	⋘	⋙	⋚	⋛	⋜	⋝	⋞	⋟
⋠	⋡	⋢	⋣	⋤	⋥	⋦	⋧	⋨	⋩	⋪	⋫	⋬	⋭	⋮	⋯
⋰	⋱

00	01	02	03	04	05	06	07	08	09	0a	0b	0c	0d	0e	0f
℀	℁	ℂ	℃	℄	℅	℆	ℇ	℈	℉	ℊ	ℋ	ℌ	ℍ	ℎ	ℏ
ℐ	ℑ	ℒ	ℓ	℔	ℕ	№	℗	℘	ℙ	ℚ	ℛ	ℜ	ℝ	℞	℟
℠	℡	™	℣	ℤ	℥	Ω	℧	ℨ	℩	K	Å	ℬ	ℭ	℮	ℯ
ℰ	ℱ	Ⅎ	ℳ	ℴ	ℵ	ℶ	ℷ	ℸ

00	01	02	03	04	05	06	07	08	09	0a	0b	0c	0d	0e	0f
			⅓	⅔	⅕	⅖	⅗	⅘	⅙	⅚	⅛	⅜	⅝	⅞	⅟
Ⅰ	Ⅱ	Ⅲ	Ⅳ	Ⅴ	Ⅵ	Ⅶ	Ⅷ	Ⅸ	Ⅹ	Ⅺ	Ⅻ	Ⅼ	Ⅽ	Ⅾ	Ⅿ
ⅰ	ⅱ	ⅲ	ⅳ	ⅴ	ⅵ	ⅶ	ⅷ	ⅸ	ⅹ	ⅺ	ⅻ	ⅼ	ⅽ	ⅾ	ⅿ
ↀ	ↁ	ↂ

00	01	02	03	04	05	06	07	08	09	0a	0b	0c	0d	0e	0f
←	↑	→	↓	↔	↕	↖	↗	↘	↙	↚	↛	↜	↝	↞	↟
↠	↡	↢	↣	↤	↥	↦	↧	↨	↩	↪	↫	↬	↭	↮	↯
↰	↱	↲	↳	↴	↵	↶	↷	↸	↹	↺	↻	↼	↽	↾	↿
⇀	⇁	⇂	⇃	⇄	⇅	⇆	⇇	⇈	⇉	⇊	⇋	⇌	⇍	⇎	⇏
⇐	⇑	⇒	⇓	⇔	⇕	⇖	⇗	⇘	⇙	⇚	⇛	⇜	⇝	⇞	⇟
⇠	⇡	⇢	⇣	⇤	⇥	⇦	⇧	⇨	⇩	⇪

00	01	02	03	04	05	06	07	08	09	0a	0b	0c	0d	0e	0f
∀	∁	∂	∃	∄	∅	∆	∇	∈	∉	∊	∋	∌	∍	∎	∏
∐	∑	−	∓	∔	∕	∖	∗	∘	∙	√	∛	∜	∝	∞	∟
∠	∡	∢	∣	∤	∥	∦	∧	∨	∩	∪	∫	∬	∭	∮	∯
∰	∱	∲	∳	∴	∵	∶	∷	∸	∹	∺	∻	∼	∽	∾	∿
≀	≁	≂	≃	≄	≅	≆	≇	≈	≉	≊	≋	≌	≍	≎	≏
≐	≑	≒	≓	≔	≕	≖	≗	≘	≙	≚	≛	≜	≝	≞	≟
≠	≡	≢	≣	≤	≥	≦	≧	≨	≩	≪	≫	≬	≭	≮	≯
≰	≱	≲	≳	≴	≵	≶	≷	≸	≹	≺	≻	≼	≽	≾	≿
⊀	⊁	⊂	⊃	⊄	⊅	⊆	⊇	⊈	⊉	⊊	⊋	⊌	⊍	⊎	⊏
⊐	⊑	⊒	⊓	⊔	⊕	⊖	⊗	⊘	⊙	⊚	⊛	⊜	⊝	⊞	⊟
⊠	⊡	⊢	⊣	⊤	⊥	⊦	⊧	⊨	⊩	⊪	⊫	⊬	⊭	⊮	⊯
⊰	⊱	⊲	⊳	⊴	⊵	⊶	⊷	⊸	⊹	⊺	⊻	⊼	⊽	⊾	⊿
⋀	⋁	⋂	⋃	⋄	⋅	⋆	⋇	⋈	⋉	⋊	⋋	⋌	⋍	⋎	⋏
⋐	⋑	⋒	⋓	⋔	⋕	⋖	⋗	⋘	⋙	⋚	⋛	⋜	⋝	⋞	⋟
⋠	⋡	⋢	⋣	⋤	⋥	⋦	⋧	⋨	⋩	⋪	⋫	⋬	⋭	⋮	⋯
⋰	⋱

00	01	02	03	04	05	06	07	08	09	0a	0b	0c	0d	0e	0f
℀	℁	ℂ	℃	℄	℅	℆	ℇ	℈	℉	ℊ	ℋ	ℌ	ℍ	ℎ	ℏ
ℐ	ℑ	ℒ	ℓ	℔	ℕ	№	℗	℘	ℙ	ℚ	ℛ	ℜ	ℝ	℞	℟
℠	℡	™	℣	ℤ	℥	Ω	℧	ℨ	℩	K	Å	ℬ	ℭ	℮	ℯ
ℰ	ℱ	Ⅎ	ℳ	ℴ	ℵ	ℶ	ℷ	ℸ

00	01	02	03	04	05	06	07	08	09	0a	0b	0c	0d	0e	0f
			⅓	⅔	⅕	⅖	⅗	⅘	⅙	⅚	⅛	⅜	⅝	⅞	⅟
Ⅰ	Ⅱ	Ⅲ	Ⅳ	Ⅴ	Ⅵ	Ⅶ	Ⅷ	Ⅸ	Ⅹ	Ⅺ	Ⅻ	Ⅼ	Ⅽ	Ⅾ	Ⅿ
ⅰ	ⅱ	ⅲ	ⅳ	ⅴ	ⅵ	ⅶ	ⅷ	ⅸ	ⅹ	ⅺ	ⅻ	ⅼ	ⅽ	ⅾ	ⅿ
ↀ	ↁ	ↂ

00	01	02	03	04	05	06	07	08	09	0a	0b	0c	0d	0e	0f
←	↑	→	↓	↔	↕	↖	↗	↘	↙	↚	↛	↜	↝	↞	↟
↠	↡	↢	↣	↤	↥	↦	↧	↨	↩	↪	↫	↬	↭	↮	↯
↰	↱	↲	↳	↴	↵	↶	↷	↸	↹	↺	↻	↼	↽	↾	↿
⇀	⇁	⇂	⇃	⇄	⇅	⇆	⇇	⇈	⇉	⇊	⇋	⇌	⇍	⇎	⇏
⇐	⇑	⇒	⇓	⇔	⇕	⇖	⇗	⇘	⇙	⇚	⇛	⇜	⇝	⇞	⇟
⇠	⇡	⇢	⇣	⇤	⇥	⇦	⇧	⇨	⇩	⇪

00	01	02	03	04	05	06	07	08	09	0a	0b	0c	0d	0e	0f
∀	∁	∂	∃	∄	∅	∆	∇	∈	∉	∊	∋	∌	∍	∎	∏
∐	∑	−	∓	∔	∕	∖	∗	∘	∙	√	∛	∜	∝	∞	∟
∠	∡	∢	∣	∤	∥	∦	∧	∨	∩	∪	∫	∬	∭	∮	∯
∰	∱	∲	∳	∴	∵	∶	∷	∸	∹	∺	∻	∼	∽	∾	∿
≀	≁	≂	≃	≄	≅	≆	≇	≈	≉	≊	≋	≌	≍	≎	≏
≐	≑	≒	≓	≔	≕	≖	≗	≘	≙	≚	≛	≜	≝	≞	≟
≠	≡	≢	≣	≤	≥	≦	≧	≨	≩	≪	≫	≬	≭	≮	≯
≰	≱	≲	≳	≴	≵	≶	≷	≸	≹	≺	≻	≼	≽	≾	≿
⊀	⊁	⊂	⊃	⊄	⊅	⊆	⊇	⊈	⊉	⊊	⊋	⊌	⊍	⊎	⊏
⊐	⊑	⊒	⊓	⊔	⊕	⊖	⊗	⊘	⊙	⊚	⊛	⊜	⊝	⊞	⊟
⊠	⊡	⊢	⊣	⊤	⊥	⊦	⊧	⊨	⊩	⊪	⊫	⊬	⊭	⊮	⊯
⊰	⊱	⊲	⊳	⊴	⊵	⊶	⊷	⊸	⊹	⊺	⊻	⊼	⊽	⊾	⊿
⋀	⋁	⋂	⋃	⋄	⋅	⋆	⋇	⋈	⋉	⋊	⋋	⋌	⋍	⋎	⋏
⋐	⋑	⋒	⋓	⋔	⋕	⋖	⋗	⋘	⋙	⋚	⋛	⋜	⋝	⋞	⋟
⋠	⋡	⋢	⋣	⋤	⋥	⋦	⋧	⋨	⋩	⋪	⋫	⋬	⋭	⋮	⋯
⋰	⋱