数式記述言語:QMath
梅谷 武
作成:2000-11-29 更新:2005-04-20
XeXで使用する数式記述言語:QMathについて定める。
IMS:20001129002; NDC:021.4; keywords:QMath, 数学記号;
目 次
1. 数式記述言語:QMath
2. qt:テキスト用数式タグ
3. qd:ディスプレイ用数式タグ
3.1 概要
3.2 命令の引数形式
3.3 Type0命令(\sqrt, \underline, …)
3.4 Type1命令(\sum, \prod, \int, …)
3.5 Type2命令(\frac, \srac, \binom, \gauss, \jacobi)
3.6 Type3命令(\array)
3.7 Type4命令(\sin, …)
3.8 Type5命令(\oplus, …)
4. qdarray:複数行数式タグ
5. eqn:番号付き数式タグ
6. eqnarray:番号付き複数行数式タグ
7. 数学記号
TeXにおいては複雑な数式がテキストとして簡単に入力できるように工夫されています。これに対して、W3Cの勧告である数式記述言語:
MATHMLは、数式をXML構文のみを使って表現しているために、これをテキストエディタで入力することは困難です。
Amayaのように専用エディタを使ってMATHMLを中間言語とする方法も考えられますが、XeXではテキストエディタによる文書作成を前提としているので、XMLタグ内に数式記述言語を埋め込むという方法を採用しました。これは
EzMathと同じ考え方です。
QMathは大雑把に、TeXにおける数式記述言語をHTML形式で実装できる程度に縮小し、さらに一部の命令をシフトJIS符号で置き換えられるようにしたものであるということができます。
XeXには次の5種類のQMath用タグがあります。
- qt → 本文内に数式を埋め込む(TeXのテキスト用数式モード'$'に対応)
- qd → 本文とは別に表示領域を確保する(ディスプレイ用数式モード'\['に対応)
- qdarray → 複数行の数式をそろえて表示する(eqnarray*環境に対応)
- eqn → qdに数式番号を付ける(equation環境に対応)
- eqnarray → qdarrayに数式番号を付ける(eqnarray環境に対応)
qtタグ内では書体はTimes Roman体になり、英字はさらに斜体となります。HTML形式では本文がsans-serif系書体に設定されているので、数式中の英数字は本文中の英数字と明確に区別することができます。XML文書の制約により、<の代わりに<を、>の代わりに>を使用します。&は数式タグ中では使用できません。
<qt>x_i, x_下, x_{i+1}</qt>xi, x下, xi+1
<qt>x^i, x^上, x^{i+1}</qt>xi, x上, xi+1
HTML形式では太字に、TeX形式では\mathbf命令に変換されます。
<qt>R^n, `R^n, `{R^n}, `実数</qt>Rn, Rn, Rn, 実数
HTML形式では上線を利用しますので、上付きや下付き命令を中に入れると線がくずれてしまいます。これに注意して使ってください。
<qt>√2, √{x^2 + y^2}, √{x_0 + y_0}</qt>√2, √x2 + y2, √x0 + y0
数式タグにおいて"\"はTeXと同様に制御文字として機能します。他の数式タグにおいてはこれに命令文字列を続けて命令として働かせることができますが、qtタグにおいてはType0, Type5命令のみが有効で、それ以外の命令は命令文字列を太字に変換します。
<qt>\ , \{, \}, \%, \$, \# \\
\sin(x) < y, y > \log(x)</qt> , {, }, %, $, #
sin(x) < y, y > log(x)<qt>\sqrt{x + y}, \underline{x + y}, \overline{x + y}</qt>√x + y, x + y, x + y
数式タグにおいて"~"はTeXと同様に明示的な空白指定として機能します。HTML形式においては半角スペースに置き換わり、"\ "は全角スペースに置き換わります。
<qt>a~b\ cdef</qt>
a b cdef
qdタグは本文とは別の領域を確保して数式をレイアウトします。HTML形式ではテーブルを利用して数式らしく表現します。構文は命令文字列が命令として解釈されること以外は、基本的にはqtタグと同様です。構文で異なる部分は、特にHTML形式でのレイアウトを制御するためにブロックという概念が導入されていることです。TeX処理系と違ってXeX処理系はHTML形式に変換する際に、数式の意味を解釈して自動的にレイアウトする機能を持ちませんので、ブロックを使って数式のレイアウトを意識的に指定する必要があります。
ブロックとはqdタグ内の連続した部分文字列であって、次のようなものです。
- {}で囲まれている
- 空白文字や{}を含まない
- 例外的に、命令がある場合はその引数文字列が終わるまでは、途中に{}や空白文字があっても連続しているとみなす。
XeX処理系は、HTML形式に変換する際に、一つのブロックをテーブルの一つの升目に配置します。
qdタグにおける命令を、その引数形式によって次のように分類することができます。
- Type0命令 + {引数文字列}
- Type1命令 + _{引数文字列} + ^{引数文字列} + {引数文字列}
- Type2命令 + {引数文字列1} + {引数文字列2}
- Type3命令 + _{左括弧文字} + ^{右括弧文字} + {行列文字列}
- Type4命令 : 引数無し
- Type5命令 : 引数無し
\sqrtは√で置き換えることができます。HTML形式における制約はqtタグと同様です。
<qd>\sqrt{2}, √{2}</qd>\underlineは下線を、\overlineは上線を引きます。
<qd>\underline{x + y}, \overline{x + y}</qd>
\sum, \prod, \sup, \inf, \limsup, \liminf, \max, \minがあります。\sumは∑(#x8794)で置き換えることができます。これはギリシャ大文字のΣ(#x83b0)とは異なりますので注意してください。
<qd>∑_{i=0}^{n}{x^i} \ \prod_{i=0}^{n}{x^i}</qd>
\intは∫(#x81e7)、\int2は∬(#x81e8)、\ointは∮(#x8793)で置き換えることができます。
<qd>∫_0^1{f(x)dx} \ ∬_D{f(x,y)dxdy} \ ∮_C{f(x,y)dx}</qd>| ∫ | 1
0 | f(x)dx | | ∬ |
D | f(x,y)dxdy | | ∮ |
C | f(x,y)dx |
\fracと\sracは分数を表現する命令です。\sracはHTML形式でのみ意味を持ち、TeX形式においては同等に機能します。\sracはHTML形式において分数の高さが間延びしてしまうことを避けるために使用します。HTML形式における\sracは中線として分母の上線もしくは分子の下線を使いますので\sqrt命令と同様に上付きや下付きを使えないという制限があります。また\frac及び\sracにおいてはその引数文字列はテキスト用数式タグで囲んだものとして扱われます。
<qd>\frac{1}{∑_{i=0}^{n}x^i} \ \srac{df}{dx}</qd>
HTML形式では連分数をTeX形式のようにきれいに表現することができません。
<qd>\frac{c_1}{b_1 + \frac{c_2}{b_2 + \frac{c_3}{b_3}}}</qd> | c1
b1 + frac{c2}{b2 + frac{c3}{b3}} |
\binomは2項係数、\gaussはガウス記号、\jacobiは平方剰余記号を表現します。
<qd>\binom{n}{k} \ \gauss{n}{k} \ \jacobi{n}{k}</qd>
\array命令で行列を表現します。デフォルトでは列の揃え方は中央揃えですが、この命令の後にc,l,rという文字を付け加えることによって(\arrayc, \arrayl, \arrayr)列の揃え方を指定することができます。引数の_命令で左括弧文字を、^命令で右括弧文字を指定できますが、これはTeX形式のみで有効です。HTML形式では行列の両側の括弧を表現することができません。
<qd>\array_{(}^{)}{
a_{11} … a_{1n} ;
: : : ;
a_{m1} … a_{mn} ;
}</qd>
Jacobi行列を書いてみます。
<qd>\array_{(}^{)}{
\frac{∂g_1}{∂x_1} … \frac{∂g_1}{∂x_n} ;
: : : ;
\frac{∂g_n}{∂x_1} … \frac{∂g_n}{∂x_n} ;
}</qd>
おもに関数を表現します。\sin, \cos, \tan, \sec, \csc, \cot, \sinh,\cosh, \tanh, \coth, \arcsin,\arccos, \arctan, \exp, \log, \mod, \max, \minがあります。HTML形式では太字に変換されます。\modはTeX形式では\bmodに変換されます。
<qd>\sin x,\ \sin(x+y),\ 3≡1(\mod~2)</qd>
| sin | x, | sin(x+y), | 3≡1(mod 2) |
特殊なフォントを表現します。\oplus, \otimes, \longrightarrow, \longmapsto,\circがあります。
<qd>a \oplus b, u \otimes v,
`R \longrightarrow `C, i \longmapsto `z, f \circ g</qd>
qdarrayタグは複数行の数式を縦方向に揃えてレイアウトします。一行の数式は、
の三つのブロックから成ります。これを続けて任意の行数の数式を表現することができます。行間は空白文字で検出しますが、強制改行"\\"を入れてもかまいません。関係子は記号や記号列からなるブロックで、これを基準にして数式を縦に揃えます。
<qdarray>
F^{-1}・F(f)(ζ^r) =
{n^{-1}∑_{t=0}^{n-1}{F(f)(ζ^t)ζ^{-tr}}} \\
{} = {n^{-1}∑_{t=0}^{n-1}{(∑_{s=0}^{n-1}{f(ζ^s)ζ^{st}})ζ^{-tr}}} \\
{} = {n^{-1}∑_{s=0}^{n-1}{f(ζ^s)(∑_{t=0}^{n-1}{ζ^{t(s-r)}})}}\\
{} = {n^{-1}f(ζ^r)(∑_{t=0}^{n-1}{ζ^0)}}\\
{} = f(ζ^r)
</qdarray>
eqnタグはqdタグと同機能で、さらに自動的に数式番号が付きます。HTML形式では"eqn"+"数式番号"というアンカーが埋め込まれます。
<eqn>S = √{s(s - a)(s - b)(s - c)}</eqn>| S | = | √s(s - a)(s - b)(s - c) |
|
eqnarrayタグはqdarrayタグと同機能で、さらに自動的に数式番号が付きます。HTML形式では"eqn"+"数式番号"というアンカーが埋め込まれます。
<eqnarray>
{\sin{α} + \sin{β}} = {2\sin{\srac{α + β}{2}}\cos{\srac{α - β}{2}}}
{\sin{α} - \sin{β}} = {2\sin{\srac{α - β}{2}}\cos{\srac{α + β}{2}}}
{\cos{α} + \cos{β}} = {2\cos{\srac{α + β}{2}}\cos{\srac{α - β}{2}}}
{\cos{α} - \cos{β}} = {-2\sin{\srac{α + β}{2}}\sin{\srac{α - β}{2}}}
</eqnarray>
XeXにおいては出力のHTML形式はXHTML1.0に準拠し、実質的な標準である
Internet Explorer 5.5と
Netscape 6で正しく表示できることと、dvi形式はpLaTeX2eで作成することを前提としています。このため使用できる数学記号は次の条件を満たすように選びました。
- シフトJIS文字集合に含まれ、かつISO/IEC 10646の定める文字集合に含まれること。
- pLaTeX2eで表示できること。
- Internet Explorer 5.5とNetscape 6で表示できること。
ただしpLaTeX2eで表示できる記号について、上記条件を満たさない場合でも必要なものはPNG形式の画像としてフォントを作成し、HTML形式で表示できるようにします。数学記号表を次のように分類して記します。
- ギリシャ小文字
- ギリシャ大文字
- 関係子
- 演算子
- 論理記号・矢印
- その他
| 表示 | TeX表記 | UCS2 | SJIS |
|---|
| α | \alpha | #x03b1 | #x83bf |
| β | \beta | #x03b2 | #x83c0 |
| γ | \gamma | #x03b3 | #x83c1 |
| δ | \delta | #x03b4 | #x83c2 |
| ε | \epsilon | #x03b5 | #x83c3 |
| ζ | \zeta | #x03b6 | #x83c4 |
| η | \eta | #x03b7 | #x83c5 |
| θ | \theta | #x03b8 | #x83c6 |
| ι | \iota | #x03b9 | #x83c7 |
| κ | \kappa | #x03ba | #x83c8 |
| λ | \lambda | #x03bb | #x83c9 |
| μ | \mu | #x03bc | #x83ca |
| ν | \nu | #x03bd | #x83cb |
| ξ | \xi | #x03be | #x83cc |
| ο | o | #x03bf | #x83cd |
| π | \pi | #x03c0 | #x83ce |
| ρ | \rho | #x03c1 | #x83cf |
| σ | \sigma | #x03c3 | #x83d0 |
| τ | \tau | #x03c4 | #x83d1 |
| υ | \upsilon | #x03c5 | #x83d2 |
| φ | \phi | #x03c6 | #x83d3 |
| χ | \chi | #x03c7 | #x83d4 |
| ψ | \psi | #x03c8 | #x83d5 |
| ω | \omega | #x03c9 | #x83d6 |
| 表示 | TeX表記 | UCS2 | SJIS |
|---|
| Α | A | #x0391 | #x839f |
| Β | B | #x0392 | #x83a0 |
| Γ | \Gamma | #x0393 | #x83a1 |
| Δ | \Delta | #x0394 | #x83a2 |
| Ε | E | #x0395 | #x83a3 |
| Ζ | Z | #x0396 | #x83a4 |
| Η | H | #x0397 | #x83a5 |
| Θ | \Theta | #x0398 | #x83a6 |
| Ι | I | #x0399 | #x83a7 |
| Κ | K | #x039a | #x83a8 |
| Λ | \Lambda | #x039b | #x83a9 |
| Μ | M | #x039c | #x83aa |
| Ν | N | #x039d | #x83ab |
| Ξ | \Xi | #x039e | #x83ac |
| Ο | O | #x039f | #x83ad |
| Π | \Pi | #x03a0 | #x83ae |
| Ρ | P | #x03a1 | #x83af |
| Σ | \Sigma | #x03a3 | #x83b0 |
| Τ | T | #x03a4 | #x83b1 |
| Υ | \Upsilon | #x03a5 | #x83b2 |
| Φ | \Phi | #x03a6 | #x83b3 |
| Χ | X | #x03a7 | #x83b4 |
| Ψ | \Psi | #x03a8 | #x83b5 |
| Ω | \Omega | #x03a9 | #x83b6 |
| 表示 | TeX表記 | UCS2 | SJIS |
|---|
| < | < | #xff1c | #x8183 |
| > | > | #xff1e | #x8184 |
| ≦ | \leqq | #x2266 | #x8185 |
| ≧ | \geqq | #x2267 | #x8186 |
| ≪ | \ll | #x226a | #x81e1 |
| ≫ | \gg | #x226b | #x81e2 |
| ⊂ | \subset | #x2282 | #x81bc |
| ⊃ | \supset | #x2283 | #x81bd |
| ⊆ | \subseteq | #x2286 | #x81ba |
| ⊇ | \supseteq | #x2287 | #x81bb |
| ∈ | \in | #x2208 | #x81b8 |
| ∋ | \ni | #x220b | #x81b9 |
| ≡ | \equiv | #x2261 | #x81df |
| ≒ | \fallingdoteq | #x2252 | #x81e0 |
| ≠ | \neq | #x2260 | #x8182 |
| ~ | \sim | #xff5e | #x8160 |
| ∝ | \propto | #x221d | #x81e5 |
| 表示 | TeX表記 | UCS2 | SJIS |
|---|
| ± | \pm | #x00b1 | #x817d |
| × | \times | #x00d7 | #x817e |
| ÷ | \div | #x00f7 | #x8180 |
| ・ | \cdot | #x30fb | #x8145 |
| ∑ | \sum | #x2211 | #x8794 |
| √ | \sqrt | #x221a | #x81e3 |
| ∂ | \partial | #x2202 | #x81dd |
| ∇ | \nabla | #x2207 | #x81de |
| ∫ | \int | #x222b | #x81e7 |
| ∬ | (\int2) | #x222c | #x81e8 |
| ∮ | \oint | #x222e | #x8793 |
| ∩ | \cap | #x2229 | #x81bf |
| ∪ | \cup | #x222a | #x81be |
| ∧ | \wedge | #x2227 | #x81c8 |
| ∨ | \vee | #x2228 | #x81c9 |
| ∠ | \angle | #x2220 | #x81da |
| ⊥ | \bot | #x22a5 | #x81db |
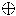 | \oplus | #x2295 | #x8853 |
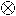 | \otimes | #x2297 | #x8855 |
| 表示 | TeX表記 | UCS2 | SJIS |
|---|
| ∀ | \forall | #x2200 | #x81cd |
| ∃ | \exists | #x2203 | #x81ce |
| ¬ | \neg | #xffe2 | #x81ca |
| ∴ | \therefore | #x2234 | #x8188 |
| ∵ | \because | #x2235 | #x81e6 |
| ← | \leftarrow | #x2190 | #x81a9 |
| ↑ | \uparrow | #x2191 | #x81aa |
| → | \rightarrow | #x2192 | #x81a8 |
| ↓ | \downarrow | #x2193 | #x81ab |
| ⇒ | \Rightarrow | #x21d2 | #x81cb |
| ⇔ | \Leftrightarrow | #x21d4 | #x81cc |
| 表示 | TeX表記 | UCS2 | SJIS |
|---|
| … | \cdots | #x2026 | #x8163 |
| ∞ | \infty | #x221e | #x8187 |
| ∥ | || | #x2225 | #x8161 |