1.4 立体幾何
著者:梅谷 武
語句:アフィン変換群,アフィン幾何,ユークリッド幾何,合同幾何,相似幾何,等積幾何,合同変換,直交群,相似変換,等積変換,運動群,回転群
立体幾何に関する用語と記号を整理する。
作成:2010-05-12
更新:2011-03-08
1.4 立体幾何
1.4.1 アフィン幾何
 空間上の変換がアフィン変換であるとは、直線図形における辺の平行性を保存することである。言い換えれば、平行六面体を平行六面体に写すことである。平行性の保存によって同値な有向線分が同値な有向線分に写されることから、アフィン変換は空間に付随するベクトル空間の変換を誘導する。

命題1.4.1.2

空間(U,V3)上のアフィン変換はベクトル空間V3上の 正則な線形変換を誘導する。
 空間(U,V3)上のアフィン変換全体の集合は写像の合成に関して群を成すが、これをアフィン変換群あふぃんへんかんぐん, affine transformation groupと呼び、Affine(U)と書く。アフィン幾何あふぃんきか, affine geometryとはアフィン変換群の構造とアフィン変換で不変な性質について調べることである。
 空間上の並進はアフィン変換であり、並進群V3はアフィン変換群Affine(U)の正規部分群であり、原点Oを固定するアフィン変換全体のなす固定部分群は一般線形群GL(V3)である。

定理1.4.1.5 アフィン変換群の構造

アフィン変換群Affine(U)は、並進群V3に内部自己同型によって一般線形群GL(V3)を作用させた半直積に同型である。
Affine(U) ≅ V3 ⋊ GL(V3)
 アフィン変換を座標を使って表現する。空間(U,V3)において正規直交性をもつアフィン標構(O;e1,e2,e3)を固定する。アフィン変換f:U → Uが与えられたとして、それに誘導される線形変換をφ:V3 → V3とし、座標原点と基底の像を座標表現する。
            f(O)
=
O + t1 e1 + t2 e2
φ(e1)
=
a11 e1 + a21 e2 + a31 e3
φ(e2)
=
a12 e1 + a22 e2 + a32 e3
φ(e3)
=
a13 e1 + a23 e2 + a33 e3
任意の点Pを与え、その点Pと像f(P)を座標表現する。
                    P
=
O + p1 e1 + p2 e2
f(P)
=
O + p1' e1 + p2' e2 + p3' e3
このとき、アフィン変換は次のように行列表現される。
lb144
p1'
p2'
p3'
1
rb144 = lb144
a11
a12
a13
t1
a21
a22
a23
t2
a31
a32
a33
t3
0
0
0
1
rb144 lb144
p1
p2
p3
1
rb144
これによりアフィン変換群Affine(U)は次のように行列表現できる。
Affine(U) = lc144 lb144
a11
a12
a13
t1
a21
a22
a23
t2
a31
a32
a33
t3
0
0
0
1
rb144 mid144 lb96
a11
a12
a13
a21
a22
a23
a31
a32
a33
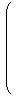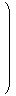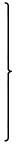
rb96 ∈ GL(3,ℝ), t1,t2,t3 ∈ ℝ rc144
ここでGL(3,ℝ)は実数上の(3,3)正則行列全体のなす群である。
 同じアフィン変換によって、アフィン標構(O;e1,e2,e3)を座標変換する。
    e1'
=
φ(e1)
e2'
=
φ(e2)
e3'
=
φ(e3)
O'
=
f(O)
とおくと、(O';e1',e2',e2')は一般には正規直交性を満たさない。任意の点Pを与え、その(O;e1,e2,e3)による座標を(p1,p2,p3)、(O';e1',e2',e3')による座標を(p1',p2',p3')とすると、次が成り立つ。
lb144
p1
p2
p3
1
rb144 = lb144
a11
a12
a13
t1
a21
a22
a23
t2
a31
a32
a33
t3
0
0
0
1
rb144 lb144
p1'
p2'
p3'
1
rb144
これによりアフィン変換を与えたときに、それによる図形変換と座標変換は互いに逆変換になっていることがわかる。
1.4.2 ユークリッド幾何
 空間上の距離や付随するベクトル空間のノルムや内積を使って図形を測るような幾何の問題を考える分野全般は、原論で展開される幾何に相当するためにユークリッド幾何ゆーくりっどきか, Euclidean geometryと呼ばれる。ユークリッド幾何はアフィン変換群の部分群である合同変換群・相似変換群・等積変換群にそれぞれ対応する合同幾何ごうどうきか, congruent geometry・相似幾何そうじきか, similar geometry・等積幾何とうせききか, equivalent geometryに分類される。

合同幾何

 空間上の合同変換ごうどうへんかん, congruent transformationとは多面体を合同な多面体に写すもののことである。特に平行六面体は平行六面体に写すことから合同変換はアフィン変換である。多面体が合同であるとは各面が合同であることであり、各面の合同条件から合同変換は空間上の距離を不変にするアフィン変換として特徴付けることができる。

定義1.4.2.4 合同変換

空間(U,V3)において、アフィン変換f:U → Uが次の条件を満たすとき、合同変換という。
(1.1)
d(P,Q) = d(f(P),f(Q)),  P,Q ∈ U

命題1.4.2.5

合同変換から誘導される線形変換はノルムと内積を保存する。
 原点Oを固定する合同変換全体のなす固定部分群は、内積を保存する線形変換の成す直交群ちょっこうぐん, orthogonal groupO(V3)である。

定理1.4.2.7 合同変換群の構造

合同変換群Cong(U)は、並進群V3に内部自己同型によって直交群O(V3)を作用させた半直積に同型である。
Cong(U) ≅ V3 ⋊ O(V3)
O(3) := { A ∈ GL(3,ℝ) ∣ tA A = A tA = E3 }
とおくと、合同変換群Cong(U)は次のように行列表現できる。
Cong(U) = lc144 lb144
a11
a12
a13
t1
a21
a22
a23
t2
a31
a32
a33
t3
0
0
0
1
rb144 mid144 lb96
a11
a12
a13
a21
a22
a23
a31
a32
a33
rb96 ∈ O(3), t1,t2,t3 ∈ ℝ rc144

相似幾何

 空間上の相似変換とは多面体を相似な多面体に写すもののことである。多面体の相似性は各面の相似性によって定義されているため、平面幾何の相似性の定義と同様に線長比と平面角の保存によって特徴付けられる。

定義1.4.2.11 相似変換

空間(U,V3)において、空間U上のアフィン変換fが相似変換そうじへんかん, similar transformationであるとは、次の条件を満たすことである。
(1) 線長比を保存する。i.e. AB:AC ∝ f(A)f(B):f(A)f(C),  ∀ A,B,C ∈ U
(2) 角度を保存する。i.e. ∠ BAC = ∠ f(B)f(A)f(C),  ∀ A,B,C ∈ U

定理1.4.2.12 相似変換群の構造

相似変換群Similar(U)は、 並進群V3に内部自己同型によって線長比のなす乗法群ℝ+と直交群O(V3)の直積を作用させた半直積に同型である。
Similar(E) ≅ V2 ⋊ (ℝ+ × O(V2))
 相似変換群Similar(U)は次のように行列表現できる。
Similar(U) =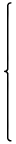
lc144 lb144
ra11
ra12
ra13
t1
ra21
ra22
ra23
t2
ra31
ra32
ra33
t3
0
0
0
1
rb144 mid144 r ∈ ℝ+,  lb96
a11
a12
a13
a21
a22
a23
a31
a32
a33
rb96 ∈ O(3), t1,t2,t3 ∈ ℝ rc144

等積幾何

 空間(U,V3)において、多面体の体積を保存するアフィン変換を等積変換とうせきへんかん, equivalent transformationという。
 等積変換群の原点の固定部分群は、外積のノルムを保存する線形変換の成す群Eq(V3)である。

定理1.4.2.18 等積変換群の構造

等積変換群Equiv(E)は、並進群V3に内部自己同型によってEq(V3)を作用させた半直積に同型である。
Equiv(E) ≅ V3 ⋊ Eq(V3)
          Eq(3,ℝ)
:=
{ A ∈ GL(3,ℝ) ∣
det A
 = 1 }
=
Eq+(3,ℝ) ∪ Eq-(3,ℝ)
Eq+(3,ℝ)
:=
{ A ∈ Eq(3,ℝ) ∣ det A = 1 }
Eq-(3,ℝ)
:=
{ A ∈ Eq(3,ℝ) ∣ det A = - 1 }
とおくとEq+(3,ℝ)はEq(3,ℝ)の正規部分群であり、特殊線形群と呼ばれ、通常SL(3,ℝ)と表記される。Eq-(3,ℝ)は部分群にはならない。等積変換群Equiv(E)は次のように行列表現できる。
Equiv(U) = lc144 lb144
a11
a12
a13
t1
a21
a22
a23
t2
a31
a32
a33
t3
0
0
0
1
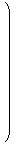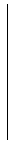
rb144 mid144 lb96
a11
a12
a13
a21
a22
a23
a31
a32
a33
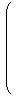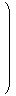rb96 ∈ Eq(3,ℝ), t1,t2,t3 ∈ ℝ rc144

運動幾何

 ユークリッド幾何における運動とは、空間上の図形を合同変換によって連続的に動かすことをいう。言い換えれば、運動とは合同変換群の単位元からの道のことである。したがって、空間における運動全体の集合、すなわち空間の運動群うんどうぐん, motion groupは合同変換群の単位元を含む弧状連結成分のことである。
 原点Oを固定する合同変換全体のなす固定部分群は、内積を保存する線形変換の成す直交群O(V3)であり、その単位元を含む弧状連結成分は原点Oを中心とする回転群SO(V3)である。

定理1.4.2.23 運動群の構造

空間における運動群Motion(U)は、並進群V3に内部自己同型によって回転群SO(V3)を作用させた半直積に同型である。
Motion(E) ≅ V3 ⋊ SO(V3)
 回転行列の全体は直交群の単位元を含む弧状連結成分であり、回転群かいてんぐん, rotation groupSO(3)と呼ばれる。
SO(3) := { A ∈ GL(3,ℝ) | tA A = A tA = E3,  det A = 1 }
運動群Motion(U)は次のように行列表現できる。
Motion(U) = lc144 lb144
a11
a12
a13
t1
a21
a22
a23
t2
a31
a32
a33
t3
0
0
0
1
rb144 mid144 lb96
a11
a12
a13
a21
a22
a23
a31
a32
a33
rb96 ∈ SO(3), t1,t2,t3 ∈ ℝ rc144
1.4.3 アフィン変換群の部分群
 アフィン変換群の部分群の包含関係をまとめると次のようになる。
 
 
Affine(E)
 
 
 
 
 
↘
 
 
↙
 
 
Equiv(E)
Similar(E)
 
 
↙
 
 
↘
 
 
 
 
 
Cong(E)
 
 
 
 
↓
 
 
 
 
Motion(E)
 
 
これらの群は並進群V3との半直積になっているので、その剰余群をとると次のようになる。
 
 
GL(V3)
 
 
 
 
 
↘
 
 
↙
 
 
Eq(V3)
ℝ+×O(V3)
 
 
↙
 
 
↘
 
 
 
 
 
O(V3)
 
 
 
 
↓
 
 
 
 
SO(V3)
 
 
1.4.4 参考文献
[1] 梅谷 武, 幾何学事始, pisan-dub.jp, 2009
数　　学
アフィン変換群 あふぃんへんかんぐん, affine transformation group
アフィン幾何 あふぃんきか, affine geometry
ユークリッド幾何 ゆーくりっどきか, Euclidean geometry
合同幾何 ごうどうきか, congruent geometry
相似幾何 そうじきか, similar geometry
等積幾何 とうせききか, equivalent geometry
合同変換 ごうどうへんかん, congruent transformation
直交群 ちょっこうぐん, orthogonal group
相似変換 そうじへんかん, similar transformation
等積変換 とうせきへんかん, equivalent transformation
運動群 うんどうぐん, motion group
回転群 かいてんぐん, rotation group
 
Published by SANENSYA Co.,Ltd.