射影直線の定義における実数を複素数に置き換えます。同時には0にならない二つの複素数の組の集合を考えます。 この集合を次のような同値関係で分類します。 この同値類を で表わすことにします。これは斉次座標あるいは同次座標と呼ばれるものです。第2成分が0でない同値類全体は と表現でき、複素平面と同じものとみなせます。第2成分が0の同値類は 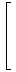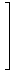と表現でき、これは無限遠点です。この同値類全体の集合 を複素射影直線ふくそしゃえいちょくせん, complex projective lineと呼びます。

 複素射影直線は平面を含みますから射影直線P¹とは異なり、無限遠直線ではなく無限遠点との和集合ですから射影平面P²とも異なります。平面幾何を拡張するための新しい空間です。

 複素射影直線P¹(ℂ)には一般線形群GL(2,ℂ)が作用します。実際に計算してみると c = 0のときは相似変換で∞は∞に写されます。 そうでないときも複素射影直線P¹(ℂ)上の全単射を引き起こします。

は複素射影直線上の恒等変換を引き起こしますが、これはGL(2,ℂ)の中心ですから、その剰余群をとって、 を複素射影直線上の複素射影変換群ふくそしゃえいへんかんぐん, complex projective transformation groupと呼びます。これは特殊線形群SL(2,ℂ)をその中心で剰余したもの に同型です。