4.1節 複素数
著者:梅谷 武
語句:複素数, 実部, 虚部, 虚数, 共役, 極形式, 偏角, 主値, 1のn乗根
平面比例として複素数を定義し、その性質について述べる。
作成:2009-09-13
更新:2021-03-28
第2章において直線上のベクトル比の比例類は対称化した線長比ℝ×に等しく、対応する相似変換群は一般線形群GL(Vα, ℝ)に等しいことを示しました。それではこれを拡張して平面上のベクトル比を考えることはできないでしょうか。ここではそれが可能であり、平面上のベクトル比の比例類は複素数の単元群ℂ×と同一視できて、平面図形の向きを保存する相似変換群ℝ+ × SO(2)とみなすことができることを示します。この意味で複素数は平面上の相似図形の比であり、複素数論とは平面比例論に他ならないということがわかります。
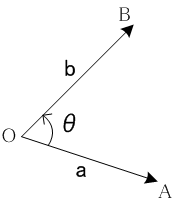
平面(E,V2)の0でないベクトルの比の集合ℛV2× :=
{ a:b | a,b ∈ V2× }
を考えます。この比例関係を比が定める相似変換が等しいこととして定義することにしましょう。
a,bに属する有向線分として原点Oを始点とするものを選ぶことにしましょう。そうするとOAをOBに写す相似変換はOAをOBと同一直線上に重ねる回転と長さを一致させる拡大縮小の合成になりますが、回転の向きが時計回りと反時計回りの二種類あります。これを反時計回りのものに決めることにしましょう。
平面上のベクトル比の比例類の代表として初項が
e1であるようなものを選ぶことができます。これにより比例類集合
RV2× := ℛV2× / ∝
はベクトル全体の集合と一対一に対応します。
RV2× ≅ V2×,
[a:b] = [e1:c]  c c
|
ここで、
c = t(x y), r = √x2 + y2とすると、変換行列は次のようになります。
ここまでの議論を整理しておきます。
Mat(ℂ) :=
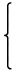
|  | | 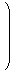 |
 x, y ∈ ℝ
x, y ∈ ℝ
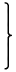 ⊂ M(2,ℝ)
⊂ M(2,ℝ)
|
は行列の積によって可換体となる。
Mat(ℂ)×により
Mat(ℂ)から零行列を除いたものを表すことにすれば、平面
(E,V2)の正規直交基底
(O;e1,e2)を定めるとき、平面上のベクトル比は
と表すことができ、図形の向きを保存する相似変換群の原点の固定部分群として平面
Eに作用する。
Mat(ℂ)は次の対応により、平面
Eあるいはベクトル空間
V2と同一視することができます。
このとき、
Mat(ℂ)×は平面
Eに行列の積によって原点の固定部分群として作用し、
Mat(ℂ)は平面
Eに行列の和によって平行移動群として作用します。
Mat(ℂ)において、
| J :=
| 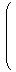 | | 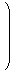 |
|
とおくと
J2 = - E2が成り立ちます。これを使うと
Mat(ℂ) = ℝ E2 ⊕ ℝ J
と直和分解できますが、
E2を
1、
Jを
iと形式的に置き換えて
ℂ := ℝ ⊕ ℝ i
という直和を作ってみましょう。そうすると
1と
iは実数体
ℝ上線形独立であり、自然に
ℝ ⊂ ℂと埋め込むことができます。この実数を拡大した体
ℂを
複素数ふくそすう, complex numberと呼びます。
ℂは
実部じつぶ, real partℝと
虚部きょぶ, imaginary partℝ iの直和ですから、任意の元
zは次のように一意的に表現できます。
| z = Re(z) + Im(z)i,
Re(z), Im(z) ∈ ℝ
|
さらに平面(E,V2)に正規直交座標系(O;e1,e2)を定めるとき、1をe1に、iをe2に対応させると、平面の座標表現E → ℝ2を実数から複素数E → ℂに置き換えることができます。
この虚数形式における計算規則を列挙しておきます。
z = a + bi, w = c + di ∈ ℂとすると、
z = a + biに対して、
z = a - biを
共役きょうやく, conjugate複素数といいます。
複素数の絶対値を
によって定義します。これは実数の絶対値の拡張になっており、複素数をベクトル空間
V2と同一視したときのノルムと一致しています。
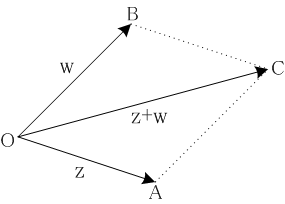
複素数をベクトルと同一視した場合、複素数の加法とベクトルの加法、複素数の減法とベクトルの減法が一致するという利点があります。これを使って平面幾何の問題を複素数の計算に帰着させることができます。
複素数z,wをベクトルとみなし、平面の原点Oからの有向線分OA,OBをそれらに属するものとするとき、それらの有向線分の和をOCとすると点Cの複素座標はz+wになります。
ベクトルの差については次が成り立ちます。
| [AB] = [OB] - [OA] = w - z
|
線分
ABを
m:nに内分する点は次のように表すことができます。
三角形
ABCの重心は次のように表すことができます。
0でない複素数
ℂ×は平面上のベクトル比全体であり、平面上の相似変換群とみなすことができ、次のように行列表現されました。
Mat(ℂ)× =
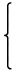 r
r
| 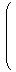 | | 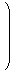 |
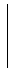 r ∈ ℝ+, θ ∈ [0,2π)
r ∈ ℝ+, θ ∈ [0,2π)
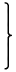
|
ここで、三角関数は弧度法を使っています。これを虚数形式で表現すると
| ℂ× = { r(cos θ + i sin θ)
∣
r ∈ ℝ+, θ ∈ [0,2π)
}
|
となります。これを
極形式きょくけいしき, polar formと呼ぶことにします。
zj = rj(cos θj + i sin θj), j=1, 2
とすると次が成り立つ。
証明
略■
z = r(cos θ + i sin θ)
とすると次が成り立つ。
証明
略■
z = r(cos θ + i sin θ)
とすると任意の整数
nに対して次が成り立つ。
S1 :=
{ cos θ + i sin θ ∣ θ ∈ [0,2π) }
は平面上の単位円を表します。自然数
nについて
とおくと
n個の複素数
| cos kθn + i sin kθn, k = 0,1,2,⋯,n-1
|
は単位円周上に等間隔に並び、単位円に内接する正
n角形の頂点となります。これらは
n乗すると
1になることから、
1のn乗根1のnじょうこん, n-th root of 1と呼ばれます。
まず、形式的冪級数環の話から始めます。形式的冪級数環の詳細については『整数論事始』[
1]を参照してください。形式的冪級数
eX,sin X,cos Xを次のように定義します。
| eX := | | ,
sin X := | | ,
cos X := | |
|
そうすると次が成り立ちます。
証明
略■
解析的な議論には深入りしませんが、上の形式的冪級数は複素平面上で絶対収束し、その結果としてオイラーの公式が導かれます。
証明
略■
なお、定義域を実数体ℝ上に制限して実関数と考えると形式的冪級数として定義したsin, cosは弧度法を使った三角関数に一致します。オイラーの公式を使って、複素数の積公式を書き直しておきます。
複素平面上の単位円S1 := { z ∈ ℂ ∣ |z| = 1 }は乗法群としてℂ×の部分群になっています。これはSO(2)を虚数形式で表現したものに他なりません。
証明
略■
[
1] 梅谷 武,
整数論事始, pisan-dub.jp, 2006
[
4] 梅沢 敏夫, 後藤 達生, 複素数と幾何学, 培風館, 1993
数 学
複素数 ふくそすう, complex number
実部 じつぶ, real part
虚部 きょぶ, imaginary part
虚数 きょすう, imaginary number
虚数単位 きょすうたんい, imaginary unit
共役 きょうやく, conjugate
極形式 きょくけいしき, polar form
偏角 へんかく, argument
主値 しゅち, principal value
1のn乗根 1のnじょうこん, n-th root of 1