3.7節 アフィン幾何の拡張
著者:梅谷 武
語句:斉次座標, 同次座標, アフィン直線, 無限遠点, 射影直線, 射影変換群, 視点, 投影線, 透視変換, 複比, 非調和比
射影直線とその上の射影変換群を定義し、アフィン変換の拡張としての射影変換の意味を視覚的に示し、複比について述べる。
作成:2009-09-11
更新:2021-03-28
3.7 アフィン幾何の拡張
3.7.1 アフィン変換群の部分群
 これまでにわかっている変換群の包含関係をまとめると次のようになります。
 
 
Affine(E)
 
 
 
 
 
↘
 
 
↙
 
 
Equiv(E)
Similar(E)
 
 
↙
 
 
↘
 
 
 
 
 
Cong(E)
 
 
 
 
↓
 
 
 
 
Motion(E)
 
 
これらの群は平行移動群Trans(E)との半直積になっているので、その剰余群をとると次のようになります。
 
 
GL(V2,ℝ)
 
 
 
 
 
↘
 
 
↙
 
 
Eq(V2,ℝ)
ℝ+×O(V2)
 
 
↙
 
 
↘
 
 
 
 
 
O(V2)
 
 
 
 
↓
 
 
 
 
SO(V2)
 
 
3.7.2 アフィン幾何の拡張
 これまでは図形が定義される平面(E,V2)を固定して、アフィン変換群の部分群で平面を等質空間としてもつ変換群が定める幾何について調べてきました。しかし、この枠組みでは遠近法で使われる射影変換をうまく表現することができません。
 そこで残りの節では平面を拡張して新しい幾何学的空間である射影平面を定義し、そこにおける幾何を定める射影変換群を決定します。射影平面には平面が、射影変換群にはアフィン変換群が自然に埋め込まれ、これによって平面幾何におけるエルランゲンプログラムが完成します。
 ここでは射影平面を定義する前に、より単純な直線上のアフィン幾何を射影直線に拡張することを考えてみます。
3.7.3 直線上のアフィン幾何
 直線(α,Vα)上に座標系(O;e)を定めると、直線上のアフィン変換f:α → αを次のように表現することができます。
                    P
=
O + xe
f(P)
=
f(O) + φ(xe)
=
O + (ax + t)e,  a ∈ ℝ× = GL(Vα,ℝ),  t ∈ ℝ = Trans(α)
=
O + x'e
これを変換前後の座標の関係式にし、
x' = ax + t
さらにまとめて行列表現していました。
lb72
x'
1
rb72 = lb72
a
t
0
1
rb72 lb72
x
1
rb72
この行列表現では、直線αを次のような集合と一対一に対応させています。
lc72 lb72
x
1
rb72 mid72 x ∈ ℝ rc72
3.7.4 射影直線
 同時には0にならない二つの実数の組の集合を考えます。
lc72 lb72
x
y
rb72 mid72 lb72
x
y
rb72 ≠ lb72
0
0
rb72,  x,y ∈ ℝ rc72
この集合を次のような同値関係で分類します。
lb72
x1
y1
rb72 ∼ lb72
x2
y2
rb72 ⇔ lb72
x1
y1
rb72 = s lb72
x2
y2
rb72 ,  s ∈ ℝ×
この同値類を
la72
x
y
ra72
で表わすことにします。これは斉次座標せいじざひょう, homogeneous coordinateあるいは同次座標どうじざひょう, homogeneous coordinateと呼ばれています。第2成分が0でない同値類全体は
A1 := lc72 la72
x
1
ra72 mid72 x ∈ ℝ rc72
と表現することができます。これは平面上の直線と同じものが埋め込まれているとみなすことができ、アフィン直線あふぃんちょくせん, affine lineと呼ばれます。第2成分が0の同値類は
∞ := la72
1
0
ra72
と表現することができ、これを無限遠点むげんえんてん, point at infinityといい、この同値類全体の集合
P1 := A1 ∪ {∞}
を射影直線しゃえいちょくせん, projective lineと呼びます。
 射影直線P1には一般線形群GL(2,ℝ)が作用します。実際に計算してみると
lb72
a
b
c
d
rb72 la72
x
1
ra72 = la72
ax + b
cx + d
ra72    lb72
a
b
c
d
rb72 la72
1
0
ra72 = la72
a
c
ra72
c = 0のときはアフィン変換で∞は∞に写されます。
la72
a
d
x + 
b
d
1
ra72    la72
1
0
ra72 ,  c = 0
そうでないときも射影直線P1上の全単射を引き起こします。
la72
ax+b
cx+d
1
ra72    la72
a
c
1
ra72 ,  c ≠ 0, x ≠ -
d
c
la72
1
0
ra72    la72
a
c
1
ra72 ,  c ≠ 0, x = -
d
c
3.7.5 射影変換群
 一次元のアフィン変換において
lc72 aE2 = lb72
a
0
0
a
rb72 mid72 a ∈ ℝ× rc72
は射影直線上の恒等変換を引き起こしますが、これはGL(2,ℝ)の 中心ですから、その剰余群をとって、
PGL(2,ℝ) := GL(2,ℝ) / ℝ×
を射影直線P1上の射影変換群しゃえいへんかんぐん, projective transformation groupと呼びます。これは特殊線形群SL(2,ℝ)をその中心で剰余したもの
PSL(2,ℝ) := SL(2,ℝ) / { E2, -E2 }
に同型です。

定理3.7.5.2 射影変換群の一意性

射影変換群PGL(2,ℝ)は次の条件を満たし、かつこれらの条件を満たす変換群はこれ以外に存在しない。
(1) 射影直線P1に推移的に作用する。
(2) 無限遠点の固定部分群はアフィン直線上のアフィン変換群Affine(A1)に一致する。

証明

略■
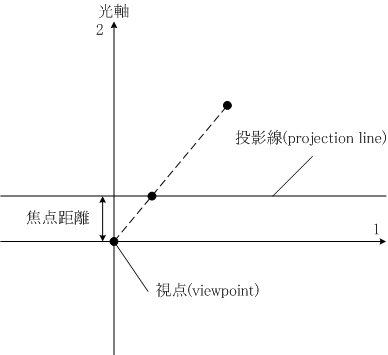
3.7.6 一次元カメラモデル
 一次元の射影変換の意味を一次元カメラモデルを使って解説しておきます。一次元カメラは原点に視点してん, viewpointを置き、y = 1を投影線とうえいせん, projection lineとして、透視変換とうしへんかん, perspective projection
la72
x
y
ra72 longmapsto la72
x
y
1
ra72
によって二次元平面上の点を投影線上に投影するものです。この変換は対象となる点をその点と視点を結ぶ直線と投影線の交点に変換します。
図3.7.6.2 一次元カメラによる透視投影
一次元カメラによる透視投影
 射影変換は、
lb72
a
b
c
d
rb72 la72
x
1
ra72 → la72
ax+b
cx+d
ra72 → la72
ax+b
cx+d
1
ra72
というように線形変換して正規化するという二段階で構成されますが、この後段の正規化が一次元カメラによる透視変換に他なりません。
3.7.7 複比
 射影直線上の射影変換は分数変換ですから線形性は成り立ちません。また射影直線上には計量が導入されていませんから、計量による不変量も考えられません。しかし、射影変換には複比あるいは非調和比と呼ばれる不変量が存在します。
 まず最初に、射影直線P1内に埋め込まれたアフィン直線上に相異なる四点P = t[p 1],  Q = t[q 1],  R = t[r 1],  S = t[s 1] が与えられたとしましょう。このとき、この四点の複比ふくひ, cross ratioあるいは非調和比ひちょうわひ, anharmonic ratioを次のように定義します。
(P,Q;R,S) :=
p-r
p-s
q-s
q-r
任意の射影変換
A = lb72
a
b
c
d
rb72 ∈ PGL(2,ℝ)
について複比が保存されることを示します。
(A(P),A(Q);A(R),A(S))
=
ap+b
cp+d
-
ar+b
cr+d
ap+b
cp+d
-
as+b
cs+d
aq+b
cq+d
-
as+b
cs+d
aq+b
cq+d
-
ar+b
cr+d
=
det A(p-r)
cr+d
det A(p-s)
cs+d
det A(q-s)
cs+d
det A(q-r)
cr+d
=
p-r
p-s
q-s
q-r
 複比の定義を射影直線P1上に拡張します。射影直線P1上に少なくとも三点が異なる四点P = t[p1 p2],  Q = t[q1 q2],  R = t[r1 r2],  S = t[s1 s2] が与えられたとしましょう。 このとき、この四点の複比を次のように定義します。
(P,Q;R,S) :=
p1r2-p2r1
p1s2-p2s1
q1s2-q2s1
q1r2-q2r1
P,Q,R,Sの中に等しい点があっても、複比は0,∞を含めれば値が定まります。

定理3.7.7.4

射影直線上の複比は射影変換に関する不変量である。

証明

略■
3.7.8 参考文献
[1] 伊原 信一郎, 河田 敬義, 線型空間・アフィン幾何 (岩波基礎数学選書), 岩波書店, 1997
[2] 佐藤 淳, コンピュータビジョン―視覚の幾何学, コロナ社, 1999
img
 
 
数　　学
斉次座標 せいじざひょう, homogeneous coordinate
同次座標 どうじざひょう, homogeneous coordinate
アフィン直線 あふぃんちょくせん, affine line
無限遠点 むげんえんてん, point at infinity
射影直線 しゃえいちょくせん, projective line
射影変換群 しゃえいへんかんぐん, projective transformation group
視点 してん, viewpoint
投影線 とうえいせん, projection line
透視変換 とうしへんかん, perspective projection
複比 ふくひ, cross ratio
非調和比 ひちょうわひ, anharmonic ratio
 
Published by SANENSYA Co.,Ltd.