3.6節 岩澤分解
著者:梅谷 武
語句:上三角行列, 剪断, 拡大縮小, 岩澤分解
一般線形群を岩澤分解することによって、アフィン変換を分類する。
作成:2009-09-10
更新:2021-03-28
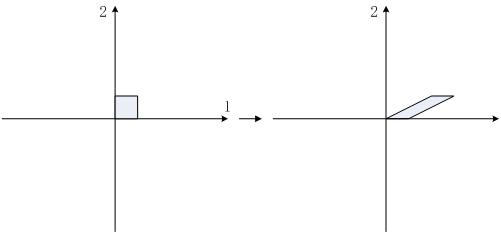
1軸に関する剪断行列全体は一般線形群
GL(2,ℝ)の部分群を成します。これを
剪断群せんだんぐん, shearing groupShear(2)と呼ぶことにします。
Shear(2) :=
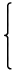
| 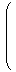 | |  |
∈ GL(2,ℝ)  r ∈ ℝ r ∈ ℝ
|
これは加法群としての
ℝに同型です。
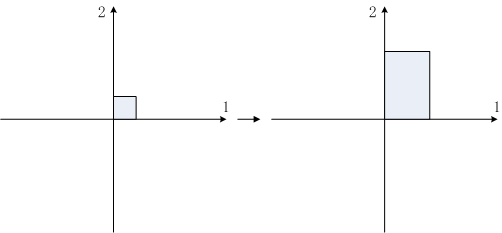
Shear(2) Scale(2)は
GL(2,ℝ)の部分群になっています。
任意の平面上のアフィン変換は次のように
(3,3)正則行列で表現される線形変換と平行移動の積に分解されます。
ですから、
(2,2)正則行列
がどのような変換であるかがわかれば、平行移動を合成することによってそのアフィン変換で図形がどのように変換されるかがわかります。
これまでの結果をまとめると(2,2)正則行列を剪断・拡大縮小・鏡映・回転の積に一意的に分解できることを証明することができます。
一般線形群
GL(2,ℝ)の任意の元は剪断・拡大縮小・鏡映・回転の積に一意的に分解することができる。すなわち、
 | | 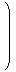 |
∈ GL(2,ℝ)
|
とすると、
r ∈ ℝ, x,y ∈ ℝ+,
θ ∈ [0,4∠R)が一意的に存在して次のいずれかが成り立つ。
これを
岩澤分解いわさわぶんかい, Iwasawa decompositionと呼ぶ。さらに、一般線形群
GL(2,ℝ)は剪断群
Shear(2)、拡大縮小群
Scale(2)、鏡映群
Ref(2)、回転群
SO(2)の直積に位相空間として同相である。
| GL(2,ℝ) ≅
Shear(2) × Scale(2) ×
Ref(2) × SO(2)
|
証明
分解の可能性と一意性はすでに示されている。同相であることの証明は省略する。■
定理の後半は群としての同型ではないことに注意してください。後の計算の都合上、本来の岩澤分解と逆の順番にしています。また、計算を簡単にするためにGram-Schmidtの直交化法ではなく、Givens回転を使っています。
[
1] K. Iwasawa, On some types of topological groups, Ann. of Math., vol.50, 507-557, 1949
数 学
上三角行列 うえさんかくぎょうれつ, upper triangular matrix
剪断 せんだん, shear
拡大縮小 かくだいしゅくしょう, scaling
剪断群 せんだんぐん, shearing group
拡大縮小群 かくだいしゅくしょうぐん, scaling group
岩澤分解 いわさわぶんかい, Iwasawa decomposition