3.4節 ユークリッド幾何
著者:梅谷 武
語句:合同変換群, 直交行列, 直交群, 特殊直交群, 回転群, 相似変換群, 等積変換群, 特殊線形群
合同幾何・相似幾何・等積幾何を定める合同変換群・相似変換群・等積変換群の構造を決定する。
作成:2009-09-08
更新:2021-03-28
平面上の
合同変換ごうどうへんかん, congruent transformationとは直線図形を合同な直線図形に写すもののことです。特に平行四辺形は平行四辺形に写しますから合同変換はアフィン変換です。命題I-8「二つの三角形において、二つの対応する辺と底辺どうしがそれぞれ等しければ、等しい辺に挟まれる角どうしはそれぞれ等しい。」により、二つの三角形の合同条件として三辺の線長量がそれぞれ等しいというものがありますから、合同変換は平面上の距離を不変にするアフィン変換として特徴付けることができます。
平面
(E,V2)において、アフィン変換
f:E → Eが合同変換であるためには次が必要十分である。
| d(P,Q) = d(f(P),f(Q)), ∀ P,Q ∈ E
|
アフィン変換fから誘導される線形変換φは、ベクトル空間V2の元aについて、有向線分AB ∈ aの端点の像をf(A) = C, f(B) = Dとするとき、有向線分CDによってφ(a) := [CD]と定めることで得られました。
合同変換は距離を不変にするので、
| d(A,B) = d(f(A),f(B)), A,B ∈ E
|
が成り立ち、有向線分の長さとして定義されるノルムについても
が成り立ちます。さらに内積とノルムの関係から、内積についても
| 〈 a, b 〉 = 〈 φ(a), φ(b) 〉,
a,b ∈ V2
|
が成り立ちます。
合同変換から誘導される線形変換はノルムと内積を保存する。
平行移動群
Trans(E)に合同変換群
Cong(E)の内部自己同型によって一般線形群
GL(V2,ℝ)の部分群である原点
Oの固定部分群
GOを作用させた半直積
Trans(E) ⋊ GOは
Cong(E)と同型である。
このことから、合同変換群の構造も原点Oの固定部分群GOの構造によって決まることがわかります。
以後、平面
(E,V2)において正規直交座標系
(O;e1,e2)を固定して考えます。合同変換
fから誘導される線形変換
φが
| A =
|  | |  |
|
と行列表現され、二つのベクトル
a,bが次のように座標表現されているとします。
| | | λ1 e1 + μ1 e2
=
|  | |  |
|
| | | λ2 e1 + μ2 e2
=
| 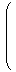 | | 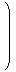 |
|
このとき内積は次のように表現されます。
| 〈 a, b 〉
=
ta b
=
( λ1 μ1 )
| 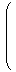 | | 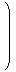 |
=
λ1 λ2 + μ1 μ2
|
これに線形変換
φを適用すると次のようになります。
ここで、特に基底を代入すると、
となり、これは行列の積
tA Aの(i,j)-成分を表していますから、
φが内積を保存することと
〈 ei, ej 〉 = δijより、
| tA A = E2 :=
| 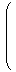 | | 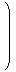 |
|
であることがわかります。
tA = A-1から
tA A = A tA = E2が成り立ちますが、このような行列は
直交行列ちょっこうぎょうれつ, orthogonal matrixと呼ばれます。
原点を固定する合同変換に誘導される線形変換の行列表現が直交行列になることを示しましたが、その計算は、逆に直交行列が原点を固定する合同変換を誘導することも示していますから、
とおくと、合同変換群の原点の固定部分群
GOは直交群
O(V2)に一致することがわかりました。
合同変換群
Cong(E)は、平行移動群
Trans(E)に内部自己同型によって直交群
O(V2)を作用させた半直積に同型である。
| Cong(E) ≅
Trans(E) ⋊ O(V2)
|
平面上の相似変換とは直線図形を相似な直線図形に写すもののことです。命題VI-4「等角な三角形において、等しい角を挟む辺どうしは比例し、それらの辺を挟む角が対応している。」と命題VI-5「二つの三角形の辺どうしが比例するとき、それらは等角であり、対応する辺に挟まれる角は等しい。」から、相似変換は「角度を保存すること」そして「線長比を保存すること」によって特徴付けられます。
平面
(E,V2)において、平面
E上のアフィン変換
fが
相似変換そうじへんかん, similar transformationであるとは、次の条件を満たすことである。
| (1)
| 線長比を保存する。i.e.
AB:AC ∝ f(A)f(B):f(A)f(C),
∀ A,B,C ∈ E
|
| (2)
| 角度を保存する。i.e.
∠ BAC = ∠ f(B)f(A)f(C),
∀ A,B,C ∈ E
|
相似変換群はアフィン変換群と同様に平行移動群と原点の固定部分群の半直積として分解されますから、相似変換群の構造は原点Oの固定部分群GOの構造によって決まります。
相似変換
fから誘導される線形変換を
φとすると、線長比と角度を保存することから次が成り立ちます。
| | | 〈 λ a, λ b 〉, λ :=
| | : | | ∈ ℝ+ |
|
| | |
の行列表現
Aを
λ-1倍すると直交行列になるので、
GOは線長比のなす乗法群
ℝ+と直交群
O(V2)の積に分解できることがわかります。さらに、
ℝ+はすべてのアフィン変換と可換なのでこの分解は群としての直積になっています。
相似変換群
Similar(E)は、平行移動群
Trans(E)に内部自己同型によって線長比のなす乗法群
ℝ+と直交群
O(V2)の直積を作用させた半直積に同型である。
| Similar(E) ≅
Trans(E) ⋊ (ℝ+ × O(V2))
|
等積変換群はアフィン変換群と同様に平行移動群と原点の固定部分群の半直積として分解されますから、等積変換群の構造は原点Oの固定部分群GOの構造によって決まります。
等積変換
fから誘導される線形変換を
φとすると、面積を保存することは外積を使って次のように表現できます。
これを行列表現すると、
となり、
であることがわかります。直交群と同じように等積変換も行列式の符号で分類します。
| | |
| | |
| | | { A ∈ Eq(2,ℝ) ∣ det A = 1 } |
|
| | | { A ∈ Eq(2,ℝ) ∣ det A = - 1 } |
|
は
Eq(2,ℝ)の正規部分群であり、
特殊線形群とくしゅせんけいぐん, special linear groupと呼ばれ、通常
SL(2,ℝ)と表記されます。
Eq-(2,ℝ)は部分群にはなりません。
これにより
が原点を固定する等積変換全体のなす群となります。
等積変換群
Equiv(E)は、平行移動群
Trans(E)に内部自己同型によって
Eq(V2,ℝ)を作用させた半直積に同型である。
| Equiv(E) ≅
Trans(E) ⋊ Eq(V2,ℝ)
|
[
1] 伊原 信一郎, 河田 敬義, 線型空間・アフィン幾何 (岩波基礎数学選書), 岩波書店, 1997
数 学
ユークリッド幾何 ゆーくりっどきか, Euclidean geometry
合同幾何 ごうどうきか, congruent geometry
相似幾何 そうじきか, similar geometry
等積幾何 とうせききか, equivalent geometry
合同変換 ごうどうへんかん, congruent transformation
合同変換群 ごうどうへんかんぐん, congruence transformation group
直交行列 ちょっこうぎょうれつ, orthogonal matrix
直交群 ちょっこうぐん, orthogonal group
特殊直交群 とくしゅちょっこうぐん, special orthogonal group
回転群 かいてんぐん, rotation group
相似変換 そうじへんかん, similar transformation
相似変換群 そうじへんかんぐん, similar transformation group
等積変換 とうせきへんかん, equivalent transformation
等積変換群 とうせきへんかんぐん, equivalent transformation group
特殊線形群 とくしゅせんけいぐん, special linear group