3.2節 アフィン変換
著者:梅谷 武
語句:アフィン変換, アフィン変換群, 平行移動群
平面上のアフィン変換を定義し、それが付随するベクトル空間上の線形変換を誘導すること、正規直交座標系を定めることによりアフィン変換が行列表現できることを述べる。
作成:2009-09-07
更新:2021-03-28
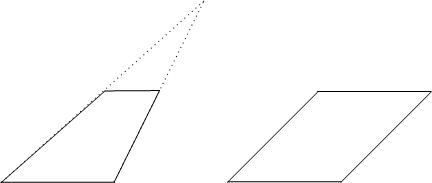
アフィン変換の例としてよく挙げられるのが源氏物語絵巻における遠近法です。西洋の遠近法は射影変換を使うために遠くのものが小さく描かれますが、源氏物語絵巻においては遠近感を出すために長方形の部屋が平行四辺形に変形されますが、遠くのものと近くのものが同じ大きさに見えます。
平行性の保存によって同値な有向線分が同値な有向線分に写されることから、アフィン変換は平面に付随するベクトル空間の変換を誘導します。
平面
(E,V2)上にアフィン変換
f:E → Eが与えられたとき、ベクトル空間
V2のベクトル
aに属する二つの有向線分
AB,CD ∈ aにおいて端点の像を
f(A)=E, f(B)=F, f(C)=G, f(D)=Hとすれば、有向線分の像は
EF,GHとなりますが、平行四辺形
ABCDの像
EFGHは平行四辺形ですから、
が成り立ちます。そこで
φ(a) := [EF]と
定めると
φは有向線分の同値類、すなわりベクトルに対して定義され、
写像
φ:V2 → V2を定めます。
アフィン変換
fに誘導された写像
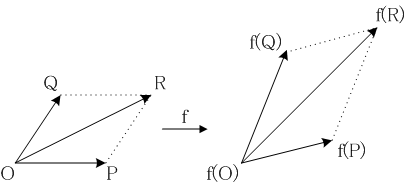
φは加法を保存します。これは、原点
Oを始点とする二つの有向線分
OP,OQについて、
とし、各端点の像を
f(O)=S, f(P)=T, f(Q)=U, f(R)=Vとすれば、平行四辺形
OPRQの像
STVUは平行四辺形ですから、
が成り立ち、
| φ([OP] + [OQ])
= φ([OP]) + φ([OQ])
|
が導かれるからです。
さらに、アフィン変換
fを平面内の直線
αに制限したとき、写像
φはその直線に付随するベクトル空間
Vαから直線
f(α)に付随するベクトル空間
Vf(α)への変換を誘導しますが、加法保存性から、
| φ( n a ) = n φ( a ), a ∈ Vα, n ∈ ℤ
|
と整数倍を保存することがわかり、このことから任意の二つのベクトル
a,b ∈ Vαについて、
が成り立ちます。なぜならば、任意の整数
m,nについて、
| φ( m a ) = m φ( a ), φ( n b ) = n φ( b )
|
となり、
| ma ⋛ nb ⇒
mφ( a ) ⋛ nφ( b )
|
が成り立つからです。順序関係の保存は包含関係の保存からわかりますから、写像
φは直線上のベクトル比を保存します。
これで写像φがベクトル空間V2上の線形変換であることがわかりましたが、アフィン変換fが全単射であることから、0でないベクトルが0に写されることはなく、φは正則です。すなわち、次の命題が証明されました。
平面
(E,V2)上のアフィン変換はベクトル空間
V2上の正則な線形変換を誘導する。
また、この証明の途中で次の補題が成り立つこともわかりました。
平面
(E,V2)においてベクトル空間
V2上の変換が加法を保存すれば、直線上のベクトル比を保存し、線形変換となる。
平面上の平行移動はアフィン変換であり、平行移動全体
Trans(E)はアフィン変換群
Affine(E)の正規部分群になり、
平行移動群へいこういどうぐん, parallel translation groupと呼ばれます。原点
Oを固定するアフィン変換全体のなす固定部分群を
GOで表します。アフィン変換
fが与えられたとき、原点
Oの
fによる像を
O'=f(O)とし、
O'を
Oに写す平行移動を
t ∈ Trans(E)とすると、
は原点
Oを固定し、しかもアフィン変換の合成ですから固定部分群
GOに含まれます。したがって、
と平行移動と原点を固定するアフィン変換に分解されます。この分解は一意的です。なぜならば、
であれば、
となり、
Trans(E) ∩ GO = { 1 }より、
t1 = t2, g1 = g2が成り立つからです。これを補題としてまとめておきます。
アフィン変換群
Affine(E)は平行移動群
Trans(E)と原点の固定部分群
GOにより、次のように分解される。
| (1)
| Affine(E) =
Trans(E)GO = { tg | t ∈ Trans(E),
g ∈ GO } |
| (2)
| Trans(E) ∩ GO = { 1 } |
アフィン変換
fに誘導される線形変換を
φとしたとき、平面上の点
Pに対して、
と定義すると、
fOは原点
Oを固定するアフィン変換であり、
O'=f(O)を
Oに写す平行移動を
t ∈ Trans(E)とすると、
と分解されます。さらにこれにより、任意の正則な線形変換から原点を固定するアフィン変換が誘導されることもわかりました。
アフィン変換を座標を使って表現してみましょう。平面
(E,V2)において正規直交座標系
(O;e1,e2)を固定して考えます。アフィン変換
f:E → Eが与えられたとして、それに誘導される線形変換を
φ:V2 → V2とし、座標原点と基底の像を座標表現します。
任意の点
Pを与え、その点
Pと像
f(P)を座標表現します。
f(P)の座標表現を計算します。
| | |
| | | O + t1 e1 + t2 e2 + p1 φ(e1) + p2 φ(e2) |
|
| | | O + t1 e1 + t2 e2 + p1 ( a11 e1 + a21 e2 )
+ p2 ( a12 e1 + a22 e2 ) |
|
| | | O + ( t1 + p1 a11 + p2 a12 ) e1
+ ( t2 + p1 a21 + p2 a22 ) e2 |
|
係数を比較すると変換前後の座標の関係がわかります。
これを行列表現します。
これは次のようにまとめて
(3,3)行列で表現することができます。
アフィン変換群
Affine(E)は正規直交座標系を定めたときに次のように行列表現できることがわかりました。
| (3.3) | Affine(E) =
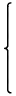
|  | |  |
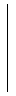
| 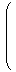 | | 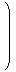 | ∈ GL(2,ℝ), t1, t2 ∈ ℝ
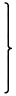
|
|
ここで
GL(2,ℝ)は実数上の
(2,2)正則行列全体のなす群です。
Affine(E)は
GL(3,ℝ)の部分群でもあります。
このアフィン変換によって、正規直交座標系
(O;e1,e2)を座標変換してみます。
とおくと、
(O';e1',e2')は一般には正規直交性を満たしませんが、平面の座標系となります。2.3節の結果により、任意の点
Pを与え、その
(O;e1,e2)による座標を
(p1, p2)、
(O';e1',e2')による座標を
(p1', p2')とすると、次が成り立ちます。
これによりアフィン変換を与えたときに、それによる図形変換と座標変換は互いに逆変換になっていることがわかります。
[
1] 伊原 信一郎, 河田 敬義, 線型空間・アフィン幾何 (岩波基礎数学選書), 岩波書店, 1997
数 学
アフィン変換 あふぃんへんかん, affine transformation
アフィン変換群 あふぃんへんかんぐん, affine transformation group
平行移動群 へいこういどうぐん, parallel translation group