5.2節 正規分布
著者:梅谷 武
語句:正規分布,Gauss分布,de Moivre-Laplaceの定理
正規分布について述べ、中心極限定理の原型であるde Moivre-Laplaceの定理をStarlingの公式を使って証明する。
作成:2012-01-27
更新:2012-02-26
5.2 正規分布
5.2.1 分布
 (ℝ,B1)上の次の密度関数fの定める分布を、平均m、分散σ2の正規分布せいきぶんぷ, normal distributionあるいはGauss分布がうすぶんぷ, Gauss distributionといい、N(m,σ2)で表わす。

密度関数

f(x) ≡
1
√2πσ
 exp lb48 －
(x－m)2
2σ2
 rb48
 これが確率測度を定めることを示す。
t =
x－m
√2σ
とおいて置換積分すると
∫ 
 
ℝ
e－t2dt
 =
∫ 
 
ℝ
e－(x－m)2/2σ2
1
√2σ
dx
であるから
∫ 
 
ℝ
f(x)dx
 =
1
√π
∫ 
 
ℝ
e－t2dt
 = 1
となる。
5.2.2 平均と分散
 te－t2は奇関数であるから
∫ 
 
ℝ
te－t2dt
 = 0
したがって

平均

∫ 
 
ℝ
xf(x)dx
 =
1
√π
∫ 
 
ℝ
(√2σt + m)e－t2dt
 = m
∫ 
 
ℝ
(x－m)2f(x)dx
=
1
√π
∫ 
 
ℝ
(2σ2t2)e－t2dt
=
2σ2
√π
la48－
t
2
e－t2ra48
∞
 
－∞
 +
σ2
√π
∫ 
 
ℝ
e－t2dt
 = σ2
したがって

分散

∫ 
 
ℝ
(x－m)2f(x)dx
 = σ2
5.2.3 積率母関数
 正規分布N(m,σ2)に従う確率変数Xの積率母関数を求める。
MX(t)
=
1
√2πσ
∫ 
 
ℝ
exp(tx) exp lb48－
(x－m)2
2σ2
rb48 dx
=
1
√2πσ
∫ 
 
ℝ
exp lb48－
1
2σ2
{(x－m)－σ2t}2 ＋ mt ＋
1
2
σ2t2 rb48 dx
=
exp lb48 mt ＋
1
2
σ2t2 rb48
1
√2πσ
∫ 
 
ℝ
exp lb48－
1
2σ2
{(x－m)－σ2t}2 rb48 dx
ここで、
y ≡
x－m
σ
 － σt
とおくと、x = σy + m + σ2tであり、
1
√2πσ
∫ 
 
ℝ
exp lb48－
1
2σ2
{(x－m)－σ2t}2 rb48 dx
=
1
√2π
∫ 
 
ℝ
exp lb48－
1
2
y2 rb48 dy
 = 1
となるから

積率母関数

MX(t) = exp lb48 mt ＋
1
2
σ2t2 rb48
5.2.4 再生性

定理5.2.4.1 正規分布の再生性

 独立な確率変数Xi, i = 1,⋯,nがそれぞれ正規分布N(mi,σi2)に従っているとき、それらの一次結合Y ≡ a0 + a1X1 + ⋯ + anXnは正規分布
N( a0 + a1m1 + ⋯ + anmn, a12σ12 + ⋯ + an2σn2 )
に従う。

証明

 Xiの積率母関数をMi(t)とおくと
MY(t)
=
exp(a0t)
n
∏
i = 1
Mi(ant)
=
exp(a0t)
n
∏
i = 1
exp lb48 aimit +
1
2
ai2σi2t2 rb48
=
exp lb48 (a0+a1m1+⋯+anmn)t +
1
2
(a12σ12+⋯+an2σn2)t2 rb48
■
5.2.5 de Moivre-Laplaceの定理
 中心極限定理により、二乗可積分な独立同分布確率変数列の第n項までの和が正規分布に法則収束することがわかっているが、これはBernoulli試行列の和が正規分布に法則収束するというde Moivre-Laplaceの定理どもあぶるらぷらすのていり, de Moivre-Laplace's theoremが発展したものである。ここではStarlingの公式を使うその古典的な証明を示す。
 成功確率pのBernoulli試行列の第n項までの和である二項分布Bin(n,p)
μSn =
n
∑
k = 0
(n
k		)
pkqn－kδk
の0≦k≦nにおける確率
(n
k		)
pkqn－k
をn → ∞のとき、Starlingの公式
n! ∼ √2πnnne－n, (n → ∞), n ∈ ℕ
で近似することを考える。
 まず単純な代入により次が得られる。
(n
k		)
pkqn－k ∼ lb48
n
2πk(n－k)
 rb481/2 lb48
np
k
 rb48k lb48
nq
n－k
 rb48n－k
x ≡ k － npとおくと右辺は
(5.1)
lb48
n
2π(np+x)(nq－x)
 rb481/2 × lb48
np
np+x
 rb48np+x lb48
nq
nq－x
 rb48nq－x
この(1)の右側の項の対数をとり、log(1+s)の級数展開を3次まで行なう。
－log lb48 lb48
np+1
np
 rb48np+x lb48
nq－x
nq
 rb48nq－x rb48
=
－(np+x)loglb48 1 +
x
np
 rb48 － (nq－x)loglb48 1 －
x
nq
 rb48
=
－(np+x)lb48
x
np
 －
x2
2n2p2
 ＋
x3
3n3p3
 + ⋯ rb48
+ (nq－x)lb48
x
np
 +
x2
2n2p2
 ＋
x3
3n3p3
 + ⋯ rb48
=
－
x2
2n
lb48
1
p
 +
1
q
 rb48 ＋
x3
6n2
lb48
1
p2
 －
1
q2
 rb48 + ⋯
これは
x3
n2
 longrightarrow 0, (n → ∞)
のとき
－log lb48 lb48
np+1
np
 rb48np+x lb48
nq－x
nq
 rb48nq－x rb48 ∼ －
x2
2npq
が成り立つ。(1)の左側の項はn → ∞で
1
√2πnpq
に近づく。ここまでの結果を補題としてまとめる。

補題5.2.5.4

 0 ＜ p ＜ 1, q ≡ 1 － pとし、0≦k≦n, k,n ∈ ℕは
(k－np)3
n2
 longrightarrow 0, (n → ∞)
を満たすとする。このとき次が成り立つ。
(n
k		)
pkqn－k ∼
1
√2πnpq
 exp lb48 －
(k－np)2
2npq
 rb48
 この補題を使って標準化した二項分布列は標準正規分布に法則収束するというde Moivre-Laplace定理を証明する。

定理5.2.5.6 de Moivre-Laplace

 0 ＜ p ＜ 1, q ≡ 1 － pとし、成功確率pのBernoulli試行列の第n項までの和をSnとするとき、次が成り立つ。
 
lim
n → ∞
Plb48 a ＜
Sn－np
√npq
 ≦ b rb48
 =
1
√2π
∫b
 
a
e－x2/2dx

証明

Plb48 a ＜
Sn－np
√npq
 ≦ b rb48
=
P(np+a√npq＜Sn≦np+b√npq)
=
 
∑
np+a√npq ＜ k ＜ np+b√npq
(n
k		)
pkqn－k
が成り立つ。
xk ≡
k－np
√npq
とおくと、a＜xk≦bより補題の条件が満たされるから、
Δxk ≡ xk+1 － xk =
1
√npq
とおけば、n → ∞のとき
Plb48 a ＜
Sn－np
√npq
 ≦ b rb48 ∼
 
∑
a ＜ xk ≦ b
1
√2π
exk2/2Δxk
この右辺は
1
√2π
∫b
 
a
e－x2/2dx
に収束する。■
 成功確率pのBernoulli試行列Xk, k =1,2,⋯の各項の平均はp、分散はpqであるから、これを標準化してn項までの和を√nで割ると
Yn
≡
1
√n
n
∑
k = 1
Xk － p
√pq
=
Sn－np
√npq
となり、de Moivre-Laplaceの定理は中心極限定理の特別な場合であることがわかる。
5.2.6 グラフ

graph005.r

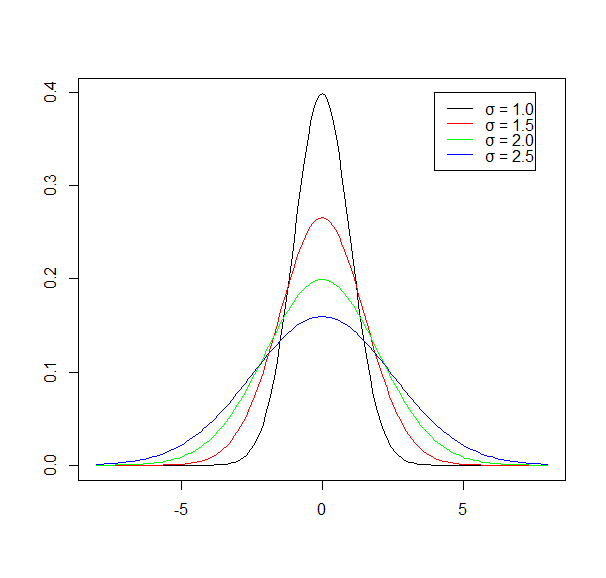
 N(0,σ2), σ = 1, 1.5, 2, 2.5を描く。
x <- seq( -8, 8, 0.1 )
plot( x, dnorm( x, 0, 1.0 ), type="l", xlab="", ylab="" )
points( x, dnorm( x, 0, 1.5 ), type="l", col="red" )
points( x, dnorm( x, 0, 2.0 ), type="l", col="green" )
points( x, dnorm( x, 0, 2.5 ), type="l", col="blue" )
legend( 4, 0.4,
  legend = c( "σ = 1.0", "σ = 1.5", "σ = 2.0", "σ = 2.5" ),
  col = c("black","red","green","blue"),
  lty = 1 )
図5.2.6.4 正規分布
正規分布

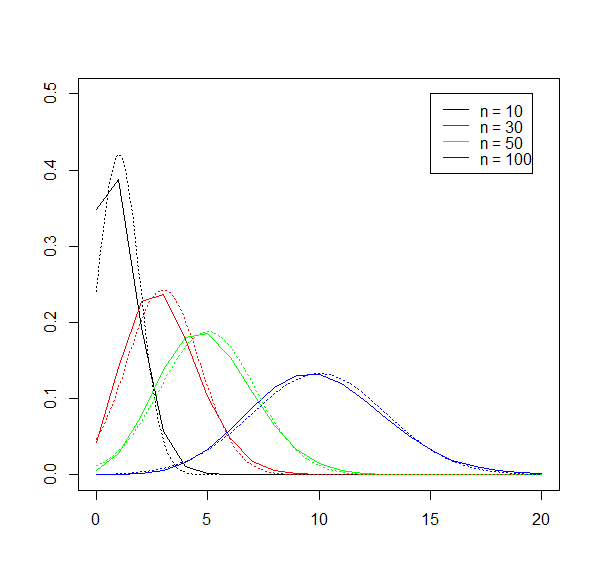
graph006.r

 Bin(n,0.1), n = 10, 30, 50, 100と平均、分散が同じ正規分布を比較する。
k <- 0:20
plot( k, dbinom( k, 10, prob=0.1 ), type="l", xlab="", ylab="",
  ylim = c( 0.0, 0.5 ) )
points( k, dbinom( k,  30, prob=0.1 ), type="l", col="red")
points( k, dbinom( k,  50, prob=0.1 ), type="l", col="green")
points( k, dbinom( k, 100, prob=0.1 ), type="l", col="blue")
par(new=T)
x <- seq(0,20,0.1)
points( x, dnorm( x, 1, sqrt(10*0.1*0.9) ), type="l",
  lty="dotted" )
points( x, dnorm( x, 3, sqrt(30*0.1*0.9) ), type="l",
  col="red", lty="dotted" )
points( x, dnorm( x, 5, sqrt(50*0.1*0.9) ), type="l",
  col="green", lty="dotted" )
points( x, dnorm( x, 10, sqrt(100*0.1*0.9) ), type="l",
  col="blue", lty="dotted" )
legend( 15, 0.5,
  legend = c( "n = 10", "n = 30", "n = 50", "n = 100" ),
  col = c("black","red","green","blue"),
  lty = 1 )
図5.2.6.8 二項分布との比較
二項分布との比較
数　　学
正規分布 せいきぶんぷ, normal distribution
Gauss分布 がうすぶんぷ, Gauss distribution
de Moivre-Laplaceの定理 どもあぶるらぷらすのていり, de Moivre-Laplace's theorem