4.3節 二項分布
著者:梅谷 武
語句:Bernoulli試行列,二項分布
有限なBernoulli試行列とその成功回数により定まる二項分布について述べる。
作成:2012-01-21
更新:2012-02-26
成功確率
p、長さ
nのBernoulli試行列について考える。
標本空間
| ΩBn ≡ { (ω1, ⋯, ωn) | ωi ∈ ΩB = {0,1},
i = 1,⋯,n }
|
事象族
 Bn ≡ Bn ≡ | n
∏
k = 1 |  B B |
|
|
|
各根元事象に対する確率は次のようになる。
| p(ω1, ⋯, ωn) = prqn-r, r ≡ | |
|
確率測度
| PBn(A) ≡ | | ,
A ∈  Bn Bn
|
(ΩBn, Bn,PBn)
Bn,PBn)上の実確率変数
Snとして成功した回数を考える。これは
Xk, k = 1,⋯,nを
k番目の成分への射影
pkとBernoulli分布の確率変数
Xとの合成
| Xk(ω1, ⋯, ωn) ≡ (X ∘ pk)(ω1, ⋯, ωn) = X(ωk)
|
とするとき、それらの和に等しい。
分布
μSnを
二項分布にこうぶんぷ, binomial distributionといい、
Bin(n,p)で表わす。
Bin(1,p)はBernoulli分布である。
平均
| | | ∫ |
ℝ
| x 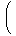
| | 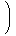 (dx) (dx) |
|
| |
|
| | |
分散は
σ2 = E[X2] - E[X]2により計算する。
| | | ∫ |
ℝ
| x2 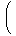
| | 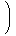 (dx) (dx) |
|
| |
|
| | |
| | |
| | | np(n-1)p + np = n(n-1)p2 + np
|
|
分散
| σ2 = E[X2] - E[X]2 = n(n-1)p2 + np - n2p2 = np(1-p) = npq
|
独立な確率変数
X, Yがそれぞれ二項分布に従うものとする。
このときそれらの和
Z ≡ X + Yも二項分布に従う。
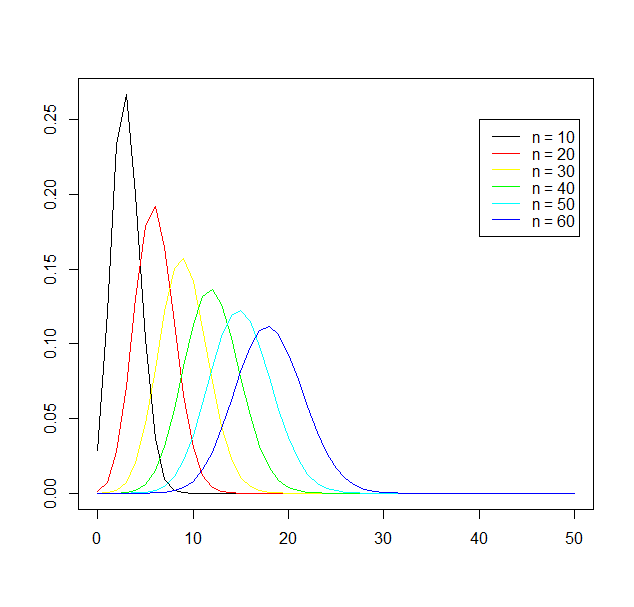
Bin(n,0.3), n = 10, 20, 30, 40, 50, 60を描く。
k <- 0:50
plot( k, dbinom( k, 10, prob=0.3 ), type="l", xlab="", ylab="" )
points( k, dbinom( k, 20, prob=0.3 ), type="l", col="red")
points( k, dbinom( k, 30, prob=0.3 ), type="l", col="yellow")
points( k, dbinom( k, 40, prob=0.3 ), type="l", col="green")
points( k, dbinom( k, 50, prob=0.3 ), type="l", col="cyan")
points( k, dbinom( k, 60, prob=0.3 ), type="l", col="blue")
legend( 40, 0.25,
legend = c( "n = 10", "n = 20", "n = 30", "n = 40",
"n = 50", "n = 60" ),
col = c("black","red","yellow","green","cyan","blue"),
lty = 1 )数 学
Bernoulli試行列 べるぬーいしこうれつ, Bernoulli trials
二項分布 にこうぶんぷ, binomial distribution
 Bn,PBn)上の実確率変数Snとして成功した回数を考える。これはXk, k = 1,⋯,nをk番目の成分への射影pkとBernoulli分布の確率変数Xとの合成
Bn,PBn)上の実確率変数Snとして成功した回数を考える。これはXk, k = 1,⋯,nをk番目の成分への射影pkとBernoulli分布の確率変数Xとの合成