4.1節 離散分布の基礎
著者:梅谷 武
語句:無限直積,δ測度,母関数,確率母関数
可算個の確率空間列に対する無限直積を定義する。無限試行列の確率空間はこれにより構成される。一次元離散分布がδ測度を使って表現できることを述べる。確率母関数で平均や分散が計算できることを述べる。
作成:2012-01-19
更新:2021-04-03
確率空間列
(Ωn, n,μn), n ∈ ℕ
n,μn), n ∈ ℕにおいて、
 ≡ ≡ 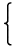 A = E × A = E × | | 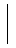 E ∈
E ∈ | n
∏
i = 1 |  i i |
|
| , n ≧ 1
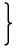
|
とおくと、

は
Ω上の有限加法族となる。
| A = E × | | ∈ 
|
に対し、
と定めると、
mは

上の有限加法的測度となる。
mは

上完全加法的である。
証明
演習とする。■
mは
σ[ ]
]上の確率測度として一意的に拡張できる。
証明
演習とする。■
δ測度
δaの分布関数はHeaviside関数
Yaである。
| Ya(x) = | 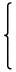 | | |
|
可測空間
(ℝ, 1)
1)上の一次元分布
μが離散分布であるための必要十分条件は位置を表わす実数列
{an}とその位置の確率を表わす正数列
{pn}が存在して次が成り立つことである。
証明
演習とする。■
可測空間
(ℝ, 1)
1)上の一次元離散分布
{μn}, μが同じ実数列
{ak}上のみに不連続点をもつとき、任意の
akについて
が成り立てば、
{μn}は
μに弱収束する。
証明
演習とする。■
無限級数として一次元離散分布を定める実数列を考えれば、それは正項級数であり、和が1となる。 したがって、その母関数の収束半径は1以上であり、アーベルの定理により[0,1]で一様収束し、項別微分可能となる。
確率母関数
fX(x)は
[0,1]で一様収束し、項別微分可能である。
証明
演習とする。■
非負整数値のみをとる確率変数
Xについて次が成り立つ。
| (ⅰ)
| E[X] = fX'(1) |
| (ⅱ)
| V[X] = fX''(1) - fX'(1)2 + fX'(1) |
証明
演習とする。■
非負整数値のみをとる独立確率変数
X,Yについて次が成り立つ。
証明
演習とする。■
数 学
無限直積 むげんちょくせき, infinite product
δ測度 でるたそくど, δ measure
母関数 ぼかんすう, generating function
確率母関数 かくりつぼかんすう, probability generating function
 n,μn), n ∈ ℕにおいて、
n,μn), n ∈ ℕにおいて、 はΩ上の有限加法族となる。
はΩ上の有限加法族となる。
 上の有限加法的測度となる。
上の有限加法的測度となる。