3.4節 中心極限定理
著者:梅谷 武
語句:弱収束,確率収束,法則収束,特性関数,中心極限定理
Borel確率測度の弱収束と分布の収束について述べる。確率密度のFourier変換である特性関数を使った中心極限定理の証明の概略を示す。
作成:2012-01-25
更新:2012-02-12
距離空間
(S,d)上のBorel確率測度
{μn}n∈ℕ, μについて次は同値である。
| (ⅰ)
| μn → μ(弱収束)
|
| (ⅱ)
| |
| (ⅲ)
| |
| (ⅳ)
| |
| (ⅴ)
| | = μ(A),
∀ A ∈  (S):μ(∂ A) = 0 (S):μ(∂ A) = 0
|
|
証明
演習とする。■
(ℝ, 1)
1)上の確率測度
{μn}n∈ℕ, μと対応する分布関数
{Fn}, Fについて次は同値である。
証明
演習とする。■
確率空間
(Ω, ,P)
,P)上の確率変数列
{Xn}n∈ℕが確率変数
Xに確率収束すれば法則収束する。
証明
演習とする。■
同一確率空間上での確率変数列の収束については
が成り立つ。
概収束、Lp収束、確率収束は一つの確率空間上の問題であるが、法則収束は異なる確率空間上の確率変数列に対しても定義することができる。これについて次の定理により、一つの確率空間内の問題に帰着できることがわかっている。
距離空間
(S,d)上のBorel確率測度
{μn}n∈ℕ, μについて、
μnが
μに弱収束するとき、ある確率空間
(Ω, ,P)
,P)上の確率変数列
{Xn}n∈ℕと確率変数
Xが存在して、
μn = μXn, μ = μXでかつ
Xnが
Xに概収束する。
証明
演習とする。■
定数と符号は異なるが実質的に特性関数はFourier変換である。
(ℝd, d)
d)上の二つの確率測度
μ,νの特性関数
φμ,φνについて
が成り立つならば
μ = νである。
証明
演習とする。■
確率空間
(Ω, ,P)
,P)上の確率変数
Xについて
| E[exp(iξX)] = φμX(ξ),
ξ ∈ ℝ
|
確率変数
X = (X1, ⋯, Xd)について
| E[exp(iξ∙x)] = φμX(ξ),
ξ ∈ ℝd
|
が成り立つ。
確率空間
(Ω, ,P)
,P)上の確率変数列
{X1, ⋯, Xn}が独立であるための必要十分条件は任意の
(ξ1, ⋯, ξn) ∈ ℝnについて、次が成り立つことである。
| E[exp(i(ξ1X1+⋯+ξnXn))] =
E[exp(iξ1X1)]⋯E[exp(iξnXn)]
|
証明
演習とする。■
(ℝd, d)
d)上の確率測度
{μn}, μについて、
μnが
μに弱収束するための必要十分条件は対応する特性関数が各点収束すること、すなわち次が成り立つことである。
証明
演習とする。■
独立で同分布をもつ二乗可積分の確率変数列
{Xn}n∈ℕにおいて、
m = E[X1], σ2 = V[X1]とする。平均
0、分散
1に標準化した確率変数の
n項までの和を
√nで割った
は標準正規分布
N(0,1)に法則収束する。
証明
証明の概略を記す。
と変換することにより、
m = 0, σ2 = 1の場合に帰着する。独立同分布であることから
| E[exp(i(ξ1Y1+⋯+ξnYn))] = E[exp(iξ1Y1)]n
|
が成り立つ。これが
N(0,1)の特性関数と等しいことを示せばよい。これは
t = ξ1とおいて
| =
exp - - | |  , t ∈ ℝ , t ∈ ℝ
|
と書くことができる。この証明は
E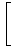 exp exp i i | | X1 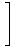 =
1 - =
1 - | | + o | |  (n → ∞) (n → ∞)
|
が成り立つことと
lim
n → ∞ |  1 - 1 - | |  n n |
|
| =
exp - | |
|
による。■
上の条件のもとで
ℝの任意の区間
(a,b]で次が成り立つ。
lim
n → ∞ | P a < a < | | ≦ b  |
|
| =
| | | |
|
数 学
弱収束 じゃくしゅうそく, weak convergent
確率収束 かくりつしゅうそく, convergent in probability
法則収束 ほうそくしゅうそく, convergent in distribution
特性関数 とくせいかんすう, characteristic function
中心極限定理 ちゅうしんきょくげんていり, central limit theorem
 ,P)上の確率変数Xについて
,P)上の確率変数Xについて