2.1節 漸近近似の基礎
著者:梅谷 武
語句:低位,高位,高々同位,同位,漸近的減少列,漸近展開,主要部,剰余,Bernoulli数,Bernoulli多項式,Euler-Maclaurinの公式,Eulerの定数
確率論では数値計算のために漸近近似の手法がよく使われる。漸近近似の基本概念であるLandauの記号と漸近展開を定義し、便利な道具であるEuler-Maclaurinの公式について述べる。次節でこの応用例としてStarlingの公式を証明する。
作成:2012-01-14
更新:2021-04-03
ℝdあるいはℝの領域D上で考える。f,gはD上の関数、aはDの内点、gはD内部のaのある近傍からaを除外した集合上で0ではないとする。このとき、xをaに近づけたときの二つの関数の関係を三種類に分類する。
a > b > 0のとき次が成り立つ。
| (ⅰ)
| log x = o(xb) (x → ∞) |
| (ⅱ)
| xb = o(xa) (x → ∞) |
| (ⅲ)
| xa = o(ex) (x → ∞) |
| (ⅰ)
| sin x ∼ x (x → 0) |
| (ⅱ)
| cos x ∼ 1 (x → 0) |
| (ⅲ)
| tan x ∼ x (x → 0) |
| (ⅳ)
| ex - 1 ∼ x (x → 0) |
ℝ上の関数
fが
aの近傍で
n-1回微分可能で
f(n)(a)が存在するときの
n次のTaylor展開
| f(x) = | | + o((x-a)n) (x → a)
|
は
fの
aにおける
n次の漸近展開である。
| (ⅰ)
| Bn(1) = Bn, n ≧ 0 |
| (ⅱ)
| Bn(0) = Bn(1) = Bn, n ≠ 1, n ≧ 0 |
| (ⅲ)
| Bn(x+1) - Bn(x) = nxn-1, n ≧ 0 |
| (ⅳ)
| Bn'(x) = nBn(x), n ≧ 1 |
| (ⅴ)
| Bn(1-x) = (-1)nBn(x), n ≧ 0 |
| (ⅵ)
| |
証明
演習とする。■
h(x)を区間
[0,1]上の
Cm級関数
(m>1)とし、部分積分の公式
を
u = B1(x), v = h(x)に適用すると
| | 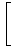 B1(x)h(x) B1(x)h(x) 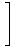 | | -
| |
|
|
| | |
右辺の末尾の積分に着目し、
u = 1/2B2(x), v = h'(x)に部分積分の公式を適用する。
| | 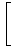 | | B2(x)h'(x)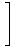 | | -
| |
|
|
これを代入して整理する。
| | | ( h(1) + h(0) ) -
| | 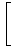 B2(x)h'(x) B2(x)h'(x) 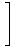 | | +
| | |
|
|
これを繰り返すことにより、次の補題が得られる。
h(x)が区間
[0,1]上の
Cm級関数
(m>1)であるとき、次が成り立つ。
a,b∈ℤ, a≦b, m∈ℕとし、区間
[a,b]上の関数
fが
Cm級であるとき、次が成り立つ。
証明
補題において
h(x) ≡ f(x + n), a ≦ n < bとし、
Bm(x-[x])により区間
[0,1]における値を使えば次が得られる。
これの
n = aから
n = b - 1までの和に
1/2(f(a) + f(b))を足せば結論が得られる。■
証明
が収束することを示せばよい。
Bm(x-[x])は
[0,1]区間の値であるから有界である。したがって
が収束するかどうかに帰着するが
| =
|
lim
n → ∞ | |  1 - 1 - | |  |
|
| = | |
|
である。■
Eulerの定数についてはよくわかっておらず、無理数かどうかも知られていない。現在は計算機により20000桁以上計算されている。
| γ = 0.57721566490153286060651209008240243 ⋯
|
[
1] 梅谷 武,
整数論事始, pisan-dub.jp, 2006
人 物
高木貞治 たかぎていじ, 1875-1960
Donald E.Knuth クヌース, 1938-
関孝和 せきたかかず, 1642?-1708
Jacob Bernoulli ヤコブ・ベルヌーイ, 1654-1705
数 学
低位 ていい, lower order
高位 こうい, higher order
高々同位 たかだかどうい, at most same order
同位 どうい, same order
漸近的減少列 ぜんきんてきげんしょうれつ, asymptotic sequence
漸近展開 ぜんきんてんかい, asymptotic expansion
主要部 しゅようぶ, principal part
剰余 じょうよ, remainder
Bernoulli数 べるぬーいすう, Bernoulli number
Bernoulli多項式 べるぬーいたこうしき, Bernoulli polynomial
Euler-Maclaurinの公式 おいらーまくろーりんのこうしき, Euler-Maclaurin's formula
Eulerの定数 おいらーのていすう, Euler's constant


