1.6節 Fourier解析
著者:梅谷 武
語句:トーラス,Fourier係数,Fourier級数,余弦係数,正弦係数,全変動,有界変動,Dirichret核,Cesàro和,Fejér核,Fourier係数,Fourier級数,Fourier変換,Fourier逆変換,Fourier変換,Fourier逆変換
Fourier解析の全体像を整理する。一変数Fourier級数についてはやや丁寧に、超関数のFourier展開まで述べる。Fourier変換についてはいろいろな関数空間の同型写像としての性質をまとめる。
作成:2012-01-05
更新:2012-02-11
一次元
トーラスとーらす, torusT ≡ ℝ/2πℤは加法に関する位相Abel群として、絶対値
1の複素数が成す乗法群である単位円と同型である。
T  S1 ≡ {z∈ℂ| S1 ≡ {z∈ℂ| | | =1}
⊂ ℂ*, t (mod 2π)  eit eit
|
一次元トーラス上の関数は実数
ℝ上の周期
2πの関数と同一視することができる。
LpノルムはFourier級数を扱いやすいよう次のように定数倍しておく。
| p ≡
 | | | |  | |
|
オイラーの公式eit = cos t + i sin tを使うとFourier級数は三角関数で表現できる。
証明
演習とする。■
f ∈ L1(T)が実数値であれば余弦係数と正弦係数は実数であり、さらに
fが偶関数ならば正弦係数は0、
fが奇関数ならば余弦係数は0となる。
証明
演習とする。■
Fourier級数は必ずしも収束するとは限らない。
とおいたとき、
がどのような関数空間で成り立つかということに関して、多くの成果が得られている。
まず、収束の十分条件については次が成り立つ。
f ∈ L1(T)のFourier係数
f(n)が
を満たせば
SN[f]は一様収束する。この条件は余弦係数
an、正弦係数
bnに関する次の条件と同等である。
証明
演習とする。■
級数の各項は連続であるから、収束すれば連続関数に収束することがわかる。関数への収束についてはLebesgueの仕事が基本となる。
有界変動関数は二つの単調非減少関数の差として表わすことができる。
証明
演習とする。■
f,g ∈ L1(T)が同じFourier級数をもてばほとんど至る所で等しい。
証明
演習とする。■
f ∈ L1(T)が有界変動であれば、各点
t ∈ Tで
特に連続点では
が成り立つ。
fが区間
[a,b]で連続かつ有界変動であれば、その内部
(a,b)に含まれる任意の閉区間上で
SN[f]は
fに一様収束する。
証明
演習とする。■
f ∈ L1(T)が区分的に滑らかであるとき、すなわち、有限個以外の点で
C1級で、
f'が区分的に連続な関数に拡張できるとき、
SN[f]は
fに一様収束する。
証明
演習とする。■
一次元トーラス
T上の
L2空間
L2(T)は内積
により定める。L.Carleson(1966)による次のものが、関数の範囲でのFourier級数の収束に関する最終的な結果である。
L2(T)において
{eint}n∈ℤは完全正規直交系であり、任意の
f ∈ L2(T)について
SN[f]は
fに
L2収束し、次が成り立つ。
証明
演習とする。■
| l2(ℤ) ≡ { {cn}n∈ℤ | cn ∈ ℂ,
| | < ∞ }
|
に次のような内積を定義する。
証明
演習とする。■
L2(T)  l2(ℤ),
f l2(ℤ),
f  {f(n)}n∈ℤ {f(n)}n∈ℤ
|
は内積空間としての同型写像であり、これにより二つの空間はユニタリ同値となる。
証明
演習とする。■
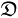 (T)
(T)は
TがコンパクトであるからFréchet空間となる。
f ∈ 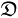 (T)
(T)のとき、
SN[f]は
fに
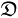 (T)
(T)の位相で収束する。
証明
演習とする。■
| S(ℤ) ≡ { {cn}n∈ℤ | cn ∈ ℂ,
| | < ∞,
∀ k > 0 }
|
は
l2(ℤ)の線形部分空間である。
証明
演習とする。■
は線形同型写像である。
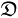 (T) ≅ S(ℤ) (T) ≅ S(ℤ)
|
証明
演習とする。■
超関数
T ∈ 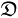 '(T)
'(T)に対するFourier係数を
により定義する。TのFourier級数展開は次のように定義する。
f ∈ 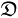 (T)
(T)を超関数と考えるとき、線形汎関数を次のように定義する。
| 〈 f, φ 〉 ≡
| | | | ,
φ ∈ 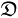 (T) (T)
|
これにより関数としてのFourier展開と超関数としてのFourier展開が一致する。
T ∈ 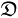 '(T)
'(T)のとき、
SN[T]は
Tに
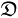 '(T)
'(T)の位相で収束する。
証明
演習とする。■
| S'(ℤ) ≡ { {cn}n∈ℤ | cn ∈ ℂ,
| | < ∞,
∃ k > 0 }
|
は線形空間であり、
l2(ℤ)はその部分空間である。
証明
演習とする。■
は線形同型写像である。
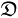 '(T) ≅ S'(ℤ) '(T) ≅ S'(ℤ)
|
証明
演習とする。■
Fejér核は
t = 1/Nとおくことで総和核になる。
証明
演習とする。■
d次元トーラス
Td ≡ (ℝ/2πℤ)dは単位円
S1の
d個の直積と同型になる。
Td  | | , (t1,⋯,td)  (eit1,⋯,eitd)
(eit1,⋯,eitd)
|
次元トーラス上の関数は実数
ℝd上の周期
2πの関数と同一視することができる。
LpノルムはFourier級数を扱いやすいよう次のように定数倍しておく。
| p ≡
 | | | |  | |
|
多変数Fourier級数は多重級数になるので、その和のとり方が一変数とは異なる。しかし、上に述べた一変数Fourier級数に関する結果はほぼそのまま成り立つ。
f ∈ L1(ℝd)について、
f(ξ)  0 ( 0 ( | |  ∞) ∞)
|
が成り立つ。
証明
演習とする。■
f,g ∈ L1(ℝd)に対し、
| f * g(ξ) = (√2π)d f(ξ)g(ξ),
ξ ∈ ℝd
|
が成り立つ。
証明
演習とする。■
証明
演習とする。■
f,g ∈ L1(ℝd), f = gならば
f = g a.e.
(√2π)d :L1(ℝd) → C0(ℝd)
:L1(ℝd) → C0(ℝd)は、畳み込みを積とするBanach環
L1(ℝd)からBanach環
C0(ℝd)への単射準同型である。
証明
演習とする。■
証明
演習とする。■
 :S(ℝd) → S(ℝd)
:S(ℝd) → S(ℝd)は連続な線形同型写像である。
証明
演習とする。■
証明
演習とする。■
L2(ℝd)におけるFourier変換は、直接定義しようとしてもFourier積分が収束するとは限らないので、L2(ℝd)で稠密なS(ℝd)の近似列を使って間接的に定義する。この近似列は適当な総和核との畳み込みにより作成する。
 :L2(ℝd) → L2(ℝd)
:L2(ℝd) → L2(ℝd)はHilbert空間としてのユニタリ同型写像である。
証明
演習とする。■
数 学
トーラス とーらす, torus
Fourier係数 ふーりえけいすう, Fourier coefficient
Fourier級数 ふーりえきゅうすう, Fourier series
余弦係数 よげんけいすう, cosine coefficient
正弦係数 せいげんけいすう, sine coefficient
全変動 ぜんへんどう, total variation
有界変動 ゆうかいへんどう, bounded variation
Dirichret核 でぃりくれかく, Dirichret kernel
Cesàro和 ちぇざろわ, Cesàro summation
Fejér核 ふぇいえーるかく, Fejér kernel
Fourier係数 ふーりえけいすう, Fourier coefficient
Fourier級数 ふーりえきゅうすう, Fourier series
Fourier変換 ふーりえへんかん, Fourier transform
Fourier逆変換 ふーりえぎゃくへんかん, Fourier inverse transform
Fourier変換 ふーりえへんかん, Fourier transform
Fourier逆変換 ふーりえぎゃくへんかん, Fourier inverse transform
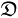 (T)を超関数と考えるとき、線形汎関数を次のように定義する。
(T)を超関数と考えるとき、線形汎関数を次のように定義する。