既約剰余類群
著者:梅谷 武
語句:ラグランジュ,バーンサイド,オイラー,方程式の代数的解法についての考察,有限群論,数論研究,有限環,既約剰余類,既約剰余類群,有限体,有限群,位数,部分群,真部分群,巡回群,右剰余類,左剰余類,指数,正規部分群,剰余類群,商群,準同型写像,同型写像,同型,核,単元群
既約剰余類群について述べる。
作成:2006-06-15
更新:2021-03-17
5.4 既約剰余類群
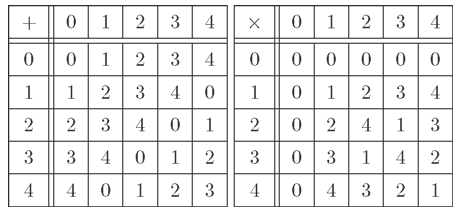
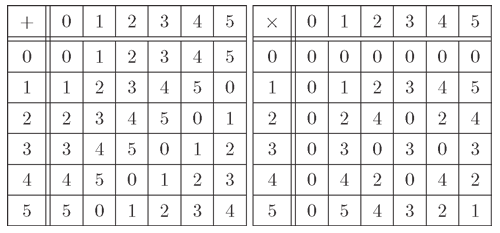
 mを正の整数としたとき、ℤ/mℤは有限集合ですから、有限な可換環という意味で有限環ゆうげんかん, finite ringでもあります。正の整数mが小さい数の場合は、すべての演算結果を表にして書き出すとその構造がよくわかります。例としてℤ/5ℤとℤ/6ℤの演算表を書いてみましょう。
表5.4.2 ℤ/5ℤの演算表
ℤ/5ℤの演算表
表5.4.3 ℤ/6ℤの演算表
ℤ/6ℤの演算表
 演算表を見てまず気が付くことは、ℤ/5ℤとℤ/6ℤの両方に共通して加法でも乗法でも右に下がる対角線に関して対称になっていることです。これは加法と乗法の可換性を表わしています。
 それから加算表に着目すると、ℤ/5ℤもℤ/6ℤも最初の行にすべての元が一回ずつ表れ、それを一つずつ巡回した行が並んでいます。これは一般に任意のa,b∈ℤ/mℤについて、
a + X = b
という一次方程式が一意的に解けると表現することができます。
 第1章において加法群を(結合律)、(零元の存在)、(逆元の存在)、(可換律)という四つの条件が成り立つこととして定義しました。このうち(零元の存在)と(逆元の存在)は「任意の二元a,bについてa + X = bを満たす解が一意的に存在する」という一つの条件に置き換えることができます。このことから加算表の各行にすべての元が一回ずつ出現しているということは、ℤ/mℤが加法群であることを意味しているということがわかります。
 ℤ/mℤの加法群としての構造は、群としてはもっとも単純な1で生成される位数mの巡回群として特徴付けられますので、mの値による違いはありません。
 乗算表の場合は、加算表とは異なりℤ/5ℤとℤ/6ℤで違いがでています。それは0行と0列を除いた部分を見るとℤ/5ℤの方には0が無いのに、ℤ/6ℤの方には0があります。これは可換環としてみたときに、ℤ/5ℤは零因子を持たず、ℤ/6ℤは零因子を持っているということです。
 ℤ/mℤの元a,bについて、a=bはa≡b(mod m)を意味します。これはa－b=mkと書けるということですから、(a,m)=(b,m)になります。つまり、ℤ/mℤの一つの剰余類aについて最大公約数(a,m)は代表元のとり方によらずに決まります。
 一般にℤ/mℤの0でない元aが零因子であることは、0でない元bが存在してa⋅b=0となることですが、これはm|abということですから、(a,m)≠1と同じことです。また、(a,m)=1であれば零因子でないだけではなく、命題5.2.3から、任意のa,b ∈ℤ/mℤについて、
a X = b
という一次方程式が一意的に解けます。
 第1章において乗法に関するアーベル群を(結合律)、(単位元の存在)、(逆元の存在)、(可換律)という四つの条件が成り立つこととして定義しました。このうち(単位元の存在)と(逆元の存在)は「任意の二元a,bについてaX = bを満たす解が一意的に存在する」という一つの条件に置き換えることができます。このことからℤ/mℤの零因子ではない元の集合は乗法に関するアーベル群を成すことがわかります。
 ここまでの議論を命題としてまとめておきます。

命題5.4.13

 剰余環ℤ/mℤの元、すなわち法mに関する剰余類aが(a,m)=1という性質をもつとき、これを法mに関する既約剰余類きやくじょうよるい, reduced residue classという。法mに関する既約剰余類全体の集合
(ℤ/mℤ)× = { a∈ℤ/mℤ | (a,m)=1 }
は乗法に関するアーベル群を成し、これを法mに関する既約剰余類群きやくじょうよるいぐん, reduced residue class groupという。

証明

 詳細は演習とする。■
 ℤ/5ℤとℤ/6ℤの乗算表から次のことがわかります。
(ℤ/5ℤ)×
=
{ 1,2,3,4 }
(ℤ/6ℤ)×
=
{ 1,5 }
(ℤ/mℤ)×の群としての構造はmの値によってさまざまに変化します。

有限体

 素数pを法とする剰余環ℤ/pℤは零因子を持たないので整域になりますが、ℤ/pℤの元は零因子でなければ単元ですので、ℤ/pℤは有限体ゆうげんたい, finite fieldになります。

命題5.4.17

 2以上の整数pについて、剰余環ℤ/pℤが整域であることとpが素数であることは同等である。

証明

 剰余環ℤ/pℤが整域であるということは零因子を持たないということである。これはa,b ∈ℤ/pℤについて 「ab = 0 ⇒ a=0またはb=0」ということであるが、これを書き直すと「p|ab ⇒ p|a または p|b」となり、定理2.5.3よりpが素数であることと同等である。■

系5.4.19

 素数pを法とする剰余環ℤ/pℤは体である。
 ℤ/5ℤ = { 0,1,2,3,4 }は有限体です。一般に素数pについて
ℤ/pℤ = { 0,1,⋯,p－1 }
は有限体となりますが、以後、これをFpと書くことにします。

群論の初歩

 ここでは可換性を仮定しないで群論のもっとも基本的な性質について述べておきます。群Gが集合として有限集合であるとき有限群ゆうげんぐん, finite groupといいます。有限群の集合としての元の個数のことを位数いすう, orderといい、|G|と書きます。有限でない群を無限群といい、無限群の位数は無限であると考えます。
 群Gの部分集合HがGの乗法に関して閉じていて、単位元1と任意の元x ∈Hの逆元x－1を含み群となっているとき部分群ぶぶんぐん, subgroupといいます。単位元のみの部分群{1}とG自身を自明な部分群といい、自明でない部分群を真部分群しんぶぶんぐん, proper subgroupといいます。

命題5.4.23

 群Gの部分集合Hが部分群であることは、任意の元x,y∈Hについてxy－1∈Hが成り立つことと同等である。

証明

 (⇒)は明らかである。(⇐)はx∈Hについてxx－1=1∈Hによって単位元を含むことがわかり、これより直ちにx－1∈Hとなり逆元を含むこともわかる。演算が閉じていることは、x,y∈Hについてy－1∈Hであり、xy=x(y－1)－1 ∈Hとなることからわかる。■
 群Gの部分集合Sについて、
＜S＞ = { x1e1 x2e2 ⋯ xkek | xi ∈S, ei ∈ℤ }
はGの部分群となりますが、これはSを含む最小の部分群となります。これをSが生成する部分群といいます。
 群Gの元aについて、＜a＞=＜{a}＞とします。
an = 1
となる自然数が存在するとき、そのような自然数の中で最小な数を元aの位数といいます。そのような自然数が存在しないとき元aの位数は無限であると考えます。＜a＞はGの部分群となりますが、その位数は元aの位数と一致します。
 群Gが一つの元から生成されるとき、すなわちa∈Gが存在してG=＜a＞となるとき、Gをaから生成される巡回群じゅんかいぐん, cyclic groupといいます。
 ℤを加法群と考えたときℤ=＜1＞となり、これは無限位数の巡回群です。任意の正の整数mに対して、ℤ/mℤを加法群と考えたときℤ/mℤ=＜1＞となり、これは位数mの巡回群です。
 (ℤ/5ℤ)× = { 1,2,3,4 }の各元の位数を計算すると
22
=
4, 23 = 3, 24 = 1
32
=
4, 33 = 2, 34 = 1
42
=
1
となります。このことから(ℤ/5ℤ)×=＜2＞=＜3＞となり、位数4の巡回群であることがわかります。また、＜4＞は位数2の真部分群であり、部分群は
{ 1 }, { 1,4 }, { 1,2,3,4 }
という三つです。
 群Gとその部分群Hが与えられたとき、G上にa－1b∈Hならばaとbを同値とする関係を定義することができます。この関係によってaとbが同値であるときaとbはHを法として右合同であるといいます。この同値関係によって群Gを分割したときの同値類を右剰余類みぎじょうよるい, right cosetといいます。右剰余類は、あるa∈Gによって
aH = { ah | h∈H }
という形で表現される集合となります。右剰余類全体の集合をG/H={aH|a∈G}と書くことにします。
 ab－1∈Hならばaとbを同値とする関係によって左合同の概念を定義することができます。この関係によってaとbが同値であるときaとbはHを法として左合同であるといいます。この同値関係によって群Gを分割したときの同値類を左剰余類ひだりじょうよるい, left cosetといいます。左剰余類は、あるa ∈Gによって
Ha = { ha | h∈H }
という形で表現される集合となります。左剰余類全体の集合を H∖G={Ha|a∈G}と書くことにします。
 群の可換性を仮定していませんので右合同と左合同の概念は一致しませんが、アーベル群の場合は右合同と左合同の概念は一致します。
 右剰余類と左剰余類の元の個数について、次のことが成り立ちます。

補題5.4.34

 群Gとその有限部分群Hについて、その任意の右剰余類aH、任意の左剰余類Hbの元の個数はHの位数|H|に等しい。

証明

 a ∈G, h,h' ∈Hについてah=ah'ならばh=h'であるから、写像H → aH, h ↦ ahは全単射である。同様に写像H → Hb, h ↦ hbも全単射である。■
 右剰余類全体の集合と左剰余類全体の集合の元の個数については次のことが成り立ちます。

補題5.4.37

 群Gとその部分群Hについて、写像G/H → H∖G, aH ↦ Ha－1は全単射となる。したがって、この二つの集合の元の個数は等しい。

証明

 aH = bHならばa－1b ∈Hであるから、Ha－1b=HよりHa－1=Hb－1が成り立つ。このことはこの写像が正しく定義されていることを意味する。同様にしてHa－1=Hb－1ならばaH = bHが成り立ち、全単射であることがわかる。■
 群Gとその部分群Hに対して、右剰余類の集合G/Hが有限集合のとき、その個数をHのGにおける指数しすう, indexといい、[G:H]と書きます。上の補題により、この定義は左剰余類の集合の個数としても同じです。無限集合のときは指数が無限であると考えます。指数と位数に関する次の式は基本的です。

定理5.4.40

 有限群Gとその部分群Hについて、次が成り立つ。
|G|=[G:H]|H|

証明

 GをHによって右剰余類の集合G/Hに分割すれば、補題によりGの位数はHの位数に右剰余類の集合G/Hの個数[G:H]をかけたものに等しいことがわかる。■
 ラグランジュLagrange, Joseph-Louis, 1736-1813は1770年に『方程式の代数的解法についての考察Rèflexions sur la rèsolution algèbrique des èquations』という論文を発表し、3次方程式と4次方程式が一般的な方法で代数的に解くことができるのに、5次以上の方程式についてはこれがうまくいかないのはなぜかということに関して考察しています。この中でラグランジュは置換群に関して系統的に調べていて、これが群論に関する最初の研究であるとされています。この論文において、置換群について次の有名なラグランジュの定理が証明されています。
 群の抽象的な定義はバーンサイドBurnside, William Snow, 1852-1927が1897年に出版した『有限群論Theory of Groups of Finite Order』において確立しました。抽象的な群論では剰余類の基本的な性質からラグランジュの定理が自然に導かれます。

系5.4.44 ラグランジュの定理

 有限群Gの部分群の位数はGの位数の約数である。
 群Gの部分群Hを法とする左右の合同関係が一致するとき、すなわち、任意の元a ∈GについてaH=Haが成り立つとき、Hを正規部分群せいきぶぶんぐん, normal subgroupといいます。正規部分群であることの条件は、任意の元a ∈Gに対してaHa－1=Hと書くことができますが、次の補題によりさらにこの条件を弱くすることができます。

補題5.4.46

 群Gの部分群Hについて、任意の元a∈Gと任意の元x∈Hに対してaxa－1∈Hが成り立てばHは正規部分群である。

証明

 この条件は任意の元a∈Gに対してaHa－1⊂Hと同じことであるから、この逆の包含関係を示せばよいが、H=a(a－1Ha)a－1⊂aHa－1からそれがわかる。■
 群論における正規部分群は、可換環論におけるイデアルのような役割を果たします。

命題5.4.49

 群Gの正規部分群Nを法とする右剰余類全体の集合G/Nの任意の剰余類aN,bNについて、その積を
(aN)(bN) = aNbN
と定義することによってG/Nは群となる。これを群Gの正規部分群Nを法とする剰余類群じょうよるいぐん, residue class groupあるいは商群しょうぐん, quotient groupという。

証明

 Nが正規部分群であることから、(aN)(bN)=aNbN=abNN=abNとなり積もまた剰余類となる。結合律はGが群であることから導かれる。単位元はNであり、 aNの逆元はa－1Nである。■
 可換環の場合と同じように、ある群の性質を調べるために、それを別の表現をもつ群へ写像で移すという手法について考えます。

定義5.4.52 群の準同型写像

 群Gから群G'への写像f:G → G'が、任意のa,b∈Gに対して、
f(ab) = f(a)f(b)
という条件を満たすとき準同型写像じゅんどうけいしゃぞう, homomorphism mapという。さらに、この準同型写像が全単射であるとき同型写像どうけいしゃぞう, isomorphism mapという。GからG'への同型写像が存在するとき、GとG'は同型どうけい, isomorphicであるといい、G≅G'と書く。
 この準同型写像に関して、可換環とまったく同じような準同型定理が成り立ちます。

補題5.4.54

 写像f:G → G'が群の準同型写像であるとき、
Ker f = f－1({1}) = { a ∈R | f(a) = 1 }
はGの正規部分群である。これをfの核かく, kernelという。

証明

 a ∈G, x ∈Ker fに対してf(gxg－1) = f(g)f(x)f(g－1) = f(g)f(g－1) = f(gg－1) = f(1) = 1.■

補題5.4.56

 写像f:G → G'が群の準同型写像であるとき、fが単射であることとKer f = {1}となることは同等である。

証明

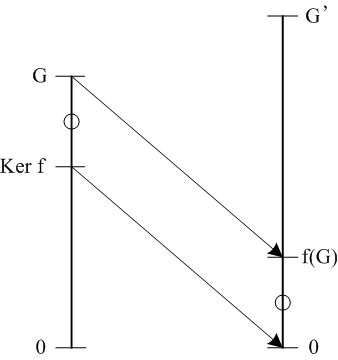
 まず、準同型写像fについてf(a)－1=f(a－1)であることに注意する。fが単射であるとはa,b ∈R, a ≠ bならばf(a)≠f(b)が成り立つことである。これをf(a)－1f(b)=f(a－1b)≠1と書き換えれば、Ker f = {1}と同じであることがわかる。■
 写像f:G → G'が群Gから群G'への準同型写像であるとき、その像f(G)はG'の部分環であり、自然な射影
π:G → G/Ker f, a ↦ a(Ker f)
fとπから自然に誘導される写像
f:G/Ker f → f(G), a(Ker f) ↦ f(a)
f(G)からG'への包含写像iによって次のような可換図式が得られます。
G─f→G'
↓π　↓i
G/Ker f─f→f(G)

定理5.4.59 群の準同型定理

 写像f:G → G'が群Gから群G'への準同型写像であるとき、その像f(G)はG'の部分群であり、fから自然に誘導される写像f:G/Ker f → f(G)は同型写像である。

証明

 まず、この写像が剰余類のとり方によらないことを示す。aがbとKer fを法として右合同であるとするとa－1b∈Ker fであるからf(a－1b)=f(a)－1f(b)=1よりf(a)=f(b)となる。f(R)が部分群であることは、その任意の元がf(a),a∈Rと書けることからわかる。写像が全射であることはあきらかである。準同型写像であることは元の写像が準同型写像であることからわかる。単射であることは、f(a(Ker f))=1はa∈Ker fを意味し、Ker f={Ker f}であることからわかる。■
図5.4.61 群の準同型定理
群の準同型定理
 k個の群G1,⋯,Gkが与えられたときに、その直積集合
G1 × ⋯ × Gk = { (a1,⋯,ak) | ai ∈Gi, i=1,⋯,k }
に乗法を
(a1,⋯,ak)(b1,⋯,bk) = (a1 b1,⋯,ak bk)
と定義すると、単位元が(1,⋯,1)であるような群になります。
 中国の剰余定理II(定理5.3.25)が与える同型写像は既約剰余類群としての同型写像を誘導します。

定理5.4.64

 m1,m2,⋯,mkを互いに素であるような正の整数としたとき、m=m1 m2 ⋯ mkとすると、写像
Φ:(ℤ/mℤ)×
→
(ℤ/m1ℤ)××⋯×(ℤ/mkℤ)×,
a(mod m)
↦
(a(mod m1),⋯,a(mod mk))
は同型写像である。

証明

 この写像によって既約剰余類が既約剰余類に対応することを示せばよい。(a,m)=1であれば(a,mi)=1, i=1,⋯,kである。逆に (ai,mi)=1, i=1,⋯,kとすると
lc144
X ≡ a1 (mod m1)
X ≡ a2 (mod m2)
⋯⋯
X ≡ ak (mod mk)
はm=m1m2⋯mkを法として一意的な解aを持ち、(a,m)=1となる。■

系5.4.66

 m = p1e1 ⋯ pkekを正の整数mの素因数分解とすれば、
(ℤ/mℤ)× ≅ (ℤ/p1e1ℤ)× × ⋯ × (ℤ/pkekℤ)×
 既約剰余類群を一般化することができます。可換環Rの単元全体の集合R×は乗法群を成し、これを可換環Rの単元群たんげんぐん, unit groupといいます。
 k個の可換環R1,⋯,Rkが与えられたときに、その直積R1 × ⋯ × Rkの単元群は
(R1 × ⋯ × Rk)× = { (a1,⋯,ak) | ai ∈Ri×, i=1,⋯,k }
となり、
(R1 × ⋯ × Rk)× ≅ R1× × ⋯ × Rk×
が成り立ちます。上の定理はこの特別な場合と考えることもできます。

オイラーの定理

 正の整数mに対して、法mの完全剰余系の中でmと互いに素であるようなものの個数φ(m)、言い換えれば、既約剰余類群(ℤ/mℤ)×の位数φ(m)を対応させる関数をオイラーのφ関数といいます。
9以下のオイラーのφ関数値
mφ(m)(ℤ/mℤ)×
11{1}
21{1}
32{1,2}
42{1,3}
54{1,2,3,4}
62{1,5}
76{1,2,3,4,5,6}
84{1,3,5,7}
96{1,2,4,5,7,8}
 φ(m)を計算しようとしたときに定理5.4.64から導かれる次の性質が有用です。このような性質を満たす関数は乗法的であるといわれます。

命題5.4.72

 m1,m2,⋯,mkを互いに素であるような正の整数としたとき、m=m1 m2 ⋯ mkとすると
φ(m) = φ(m1)φ(m2) ⋯ φ(mk)
特にm = p1e1 ⋯ pkekを正の整数mの素因数分解とすれば、
φ(m) = φ(p1e1) ⋯ φ(pkek)
 この性質からφ(m)を計算するには、素数pに対してその冪乗pkに対するオイラーのφ関数の値φ(pk)が求まればいいということがわかります。

命題5.4.74

 素数pと正の整数kについて、φ(pk) = pk－1(p－1)

証明

 法pkに関する剰余類の集合{ 1,2, ⋯,pk }においてpの倍数の全体の集合は { p,2p,3p,⋯,pk－1p }となるから、その個数はpk－1個である。したがって既約剰余類の個数が剰余類全体の個数からこれを引いたものになる。つまり、φ(pk) = pk － pk－1 = pk－1(p－1).■
 この公式から任意の正の整数mに対するオイラーのφ関数の計算公式が得られます。

系5.4.77

 m=p1e1 ⋯ pkekを正の整数mの素因数分解とすれば、
φ(m) = m lb48
1
－
1
p1
rb48 ⋯ lb48
1
－
1
pk
rb48
 オイラーEuler, Leonhard, 1707-1783は1750年頃から整数論の研究を始めたとされています。その草稿は死後に発見されて1849年に『数論研究Tractatus de numerorum doctria』として出版されました。その中で整数の約数の和を表わすσ関数やφ関数という数論的関数の計算や法によって整数を剰余類に分割し、その剰余類に対して和や積がうまく定義できることを示しています。つまり、オイラーは整数の剰余環の概念に達していました。さらに、法mと互いに素であるような数aに対して、その冪乗1,a,a2,a3,⋯がいつ1と合同になるのかについて考察し、オイラーの定理と呼ばれている次の定理を得ました。

定理5.4.79 オイラー

 正の整数mとmと互いに素であるような整数aが与えられたとき、次が成り立つ。
aφ(m) ≡ 1 (mod m)

証明

 仮定より、剰余類aは法mに関する既約剰余類群(ℤ/mℤ)×に含まれる。aの位数はラグランジュの定理(系5.4.44)により、φ(m)の約数であることより結論が従う。■
 フェルマーは1640年10月18日付けのフレニクル宛書簡の中で、オイラーの定理の素数の場合について述べています。このことから次の系はフェルマーの小定理と呼ばれています。

系5.4.82 フェルマーの小定理

 素数pとpと互いに素であるような整数aが与えられたとき、次が成り立つ。
ap－1 ≡ 1 (mod p)

久留島義太の業績

(原稿未完成)

参考文献

[1] 原田 耕一郎, 群の発見 (数学、この大きな流れ), 岩波書店, 2001
img
 
 
[2] 平井 武, 線形代数と群の表現〈1〉, 朝倉書店, 2001
img
 
 
[3] 近藤 武, 群論, 岩波書店, 2002
img
 
 
[4] カール・フリードリヒ ガウス, ガウス 整数論, 朝倉書店, 1995
img
 
 
[5] アンドレ ヴェイユ, 数論―歴史からのアプローチ, 日本評論社, 1987
img
 
 
[6] ヴィクター・J. カッツ, カッツ 数学の歴史, 共立出版, 2005
img
 
 
人　　物
ラグランジュ Lagrange, Joseph-Louis, 1736-1813
イタリア生まれの数学者、天文学者。解析力学の創始者。
バーンサイド Burnside, William Snow, 1852-1927
オイラー Euler, Leonhard, 1707-1783
スイス生まれの数学者、物理学者、天文学者。解析学、代数学、幾何学、整数論において膨大な業績を残す。歴史上もっとも多産な数学者であるといわれている。
 
物　　品
方程式の代数的解法についての考察 Rèflexions sur la rèsolution algèbrique des èquations
有限群論 Theory of Groups of Finite Order
数論研究 Tractatus de numerorum doctria
 
数　　学
有限環 ゆうげんかん, finite ring
既約剰余類 きやくじょうよるい, reduced residue class
既約剰余類群 きやくじょうよるいぐん, reduced residue class group
有限体 ゆうげんたい, finite field
有限群 ゆうげんぐん, finite group
位数 いすう, order
部分群 ぶぶんぐん, subgroup
真部分群 しんぶぶんぐん, proper subgroup
巡回群 じゅんかいぐん, cyclic group
右剰余類 みぎじょうよるい, right coset
左剰余類 ひだりじょうよるい, left coset
指数 しすう, index
正規部分群 せいきぶぶんぐん, normal subgroup
剰余類群 じょうよるいぐん, residue class group
商群 しょうぐん, quotient group
準同型写像 じゅんどうけいしゃぞう, homomorphism map
同型写像 どうけいしゃぞう, isomorphism map
同型 どうけい, isomorphic
核 かく, kernel
単元群 たんげんぐん, unit group
 
Published by SANENSYA Co.,Ltd.