剰余環
著者:梅谷 武
語句:剰余環,準同型写像,同型写像,同型,核,包含写像,標数
剰余環について述べる。
作成:2006-06-11
更新:2021-03-17
正の整数
mを法として整数を分割した剰余類の集合を
と書くことにします。この集合上で加法と乗法を
と定義することができます。
命題5.1.8はこの定義が剰余系のとり方によらずに定まることを示しています。
ℤ/mℤはこの加法と乗法に関して可換環になっています。
証明
命題5.1.8と同様にして
a ≡ b (mod I), c ≡ d (mod I)のとき、
a + c ≡ b + d (mod I), ac ≡ bd (mod I)を示すことができる。これは加法と乗法の定義が剰余系のとり方によらずに定まることを意味している。可換環の性質を満たすことは元の演算がその性質を満たしていることからわかる。■
ℤ/mℤはℤのイデアル(m)=mℤを法とする剰余環ですが、これをℤの法mに関する剰余環ともいいます。
次にある可換環の性質を調べるために、それを別の表現をもつ可換環へ写像で移すという手法について考えます。このときに使う写像は加法と乗法を保つものでなければなりません。
二つの可換環が同型であるときには、その加法や乗法に関する代数的な議論をしている限りはまったく同じものと考えてかまいません。
写像
f:R → R'が可換環の準同型写像であるとき、
| Ker f = f-1({0}) = { a ∈R | f(a) = 0 }
|
は
Rのイデアルである。これを
fの
核かく, kernelという。
証明
f(a)=f(b)=0ならばf(a+b)=f(a)+f(b)=0.f(a)=0ならばr∈Rについてf(ra)=f(r)f(a)=0.■
写像
f:R → R'が可換環の準同型写像であるとき、
fが単射であることと
Ker f = {0}となることは同等である。
証明
fが単射であるとはa,b∈R, a≠bならばf(a)≠f(b)が成り立つことである。これをf(a-b)≠0と書き換えれば、Ker f = {0}と同じであることがわかる。■
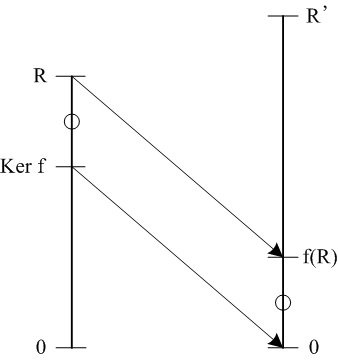
写像
f:R → R'が可換環
Rから可換環
R'への準同型写像であるとき、その像
f(R)は
R'の部分環であり、自然な射影
fと
πから自然に誘導される写像
| f:R/Ker f → f(R), a ↦ f(a)
|
から
R'への
包含写像ほうがんしゃぞう, inclusion mappingiによって次のような可換図式が得られます。
| R | ─f→ | R' |
| ↓π | | ↓i |
| R/Ker f | ─f→ | f(R) |
写像
f:R → R'が可換環
Rから可換環
R'への準同型写像であるとき、その像
f(R)は
R'の部分環であり、
fから自然に誘導される写像
f:R/Ker f → f(R)は同型写像である。
証明
まず、この写像が剰余系のとり方によらないことを示す。a≡b(mod Ker f)とするとa-b ∈Ker fであるからf(a-b)=f(a)-f(b)=0よりf(a)=f(b)となる。f(R)が部分環であることは、その任意の元がf(a), a ∈Rと書けることからわかる。写像が全射であることはあきらかである。準同型写像であることは元の写像が準同型写像であることからわかる。単射であることは、f(a)=0はa ∈Ker fを意味し、Ker f=0=Ker fであることからわかる。■
可換環
Rにおいて任意の自然数
kに対して、
とし、整数
ℤから
Rへの写像を
| ℤ ∋k ↦
|  | | |
|
によって定めるとこれは準同型写像となります。この核は
ℤのイデアルですが、
ℤは単項イデアル整域ですから、ある自然数
nが一意的に定まって
(n)=nℤと一致します。このようにして定まる自然数
nを
Rの
標数ひょうすう, characteristicといいます。準同型定理から任意の可換環はその標数を
nとすると
ℤ/nℤと同型な部分環を含むことがわかります。
可換環Rの標数が0のときは、この準同型写像は単射になりますのでRはℤと同型な部分環を含むことになります。さらにRが順序環であるときこの同型写像は順序を保ちます。このことから有理整数環ℤを次のように特徴付けることができます。
有理整数環
ℤは最小の順序環である。すなわち、任意の順序環に順序を保つ同型写像によって埋め込むことができる。
証明
演習とする。■
標数が0の体kについては、有理整数環ℤの埋め込み写像を自然に有理数体ℚへ拡張することができます。さらにkが順序体であるときこの同型写像は順序を保ちます。このことから有理数体ℚを次のように特徴付けることができます。
有理数体
ℚは最小の順序体である。すなわち、任意の順序体に順序を保つ同型写像によって埋め込むことができる。
証明
演習とする。■
可換環
Rの標数
nが正のときには、順序環の性質(O4):任意の
x,y,z ∈Rに対し、
が満たされないので
Rは順序環にはなり得ません。
k個の環
R1,⋯,Rkが与えられたときに、その直積集合
| R1 × ⋯ × Rk = { (a1,⋯,ak) | ai ∈Ri, i=1,⋯,k }
|
に加法と乗法を
と定義すると、零元は
(0,⋯,0)で、単位元は
(1,⋯,1)であるような環になります。中国の剰余定理は剰余環と直積の概念を使って次のように言い換えることができます。
m1,m2,⋯,mkを互いに素であるような正の整数としたとき、
m=m1 m2 ⋯ mkとすると、写像
| Φ:ℤ/mℤ → ℤ/m1ℤ×⋯×ℤ/mkℤ, a(mod m) ↦ (a(mod m1),⋯,a(mod{mk})
|
は同型写像である。
証明
a≡b(mod m)であれば任意の
miについて
a≡b(mod mi)であるから、この写像の定義に問題は無い。この写像の核の元
aは、任意の
miについて
a≡0(mod mi)を満たすので
a≡0(mod m)となり、
Φが単射であることがわかる。
ℤ/m1ℤ×⋯×ℤ/mkℤの任意の元
(a(mod m1),⋯,a(mod{mk})が与えられたとき、中国の剰余定理から、
は
m = m1m2⋯mkを法として一意的な解
aを持つことから
Φが全射であることがわかる。■
m = p1e1⋯pkekを正の整数
mの素因数分解とすれば、
| ℤ/mℤ ≅ ℤ/p1e1ℤ × ⋯ × ℤ/pkek ℤ
|
一回に一桁の四則演算ができる演算器をもつ計算機で、n桁の数の四則演算を計算することを考えましょう。特にn桁の乗算をするためには演算器をn2回動作させなければなりません。しかし、もしn=n1 n2 ⋯ nk, ni<n, i= 1,⋯,kというように互いに素でnよりも小さな法の組に分解したとすれば、n桁の乗算は、演算器をn回だけ動作させればいいことになります。これは変換の手間を考慮しても計算量としては相当な差になりますので、巨大な数の乗算においてはこの法算術は重要な技法となります。
加法については法算術によって計算量を減らすことができないように思われますが、法算術に変換することによって桁上がりがなくなるために、すべての桁の加算が同時並行してできるという利点があります。したがって、計算機を高度に並列化しようとしたときに、数の四則演算を法算術で行うという設計技法が有力になる可能性もあると考えられます。
中国の剰余定理は、さらに一般の可換環にまで拡張することができます。有理整数環
ℤあるいはより一般的に単項イデアル整域
Rにおいては、任意の元
a,b∈Rについて
(a) + (b) = (d)となる最大公約元
dが単元倍を除いて定まり、特に
d=1のときは
aと
bはの公約元は単元だけで
(a) + (b) = Rとなり、このとき
aと
bは
互いに素であると定義しました。これを一般の可換環のイデアルに拡張します。可換環
Rにおいて、二つのイデアル
I,Jが互いに素であるということを
によって定義します。そうすると中国の剰余定理を次のように一般の可換環に拡張することができます。
I1,I2,⋯,Ikを可換環
Rの互いに素であるようなイデアルとすると、
であり、これを
Iとおくと写像
| Φ:R/I → R/I1×⋯×R/Ik, a(mod I) ↦ (a(mod I1),⋯,a(mod{Ik})
|
は同型写像である。
証明
まず
I1と
I2が互いに素であれば
I1 ∩I2 = I1 I2であることを示す。イデアルであることから
I1I2⊂I1, I1 I2⊂I2であり、
I1I2⊂I1∩I2はつねに成り立っている。
a∈I1∩I2に対して
1=b1+b2, b1∈I1, b2∈I2をかけると
a=ab1+ab2となり、
a∈I1I2であることがわかる。したがって
I1∩I2⊂I1I2である。
次に
I1と
I2I3が互いに素であることを示す。
1=b1+b2=c1+c3, b1,c1∈I1, b2∈I2, c3∈I3とする。
| 1 = (b1+b2)(c1+c3) = b1c1 + c1b2 + b1c3 + b2c3
|
において、
b1c1+c1b2+b1c3∈I1, b2c3∈I2I3より互いに素である。このことから、
| I1 ∩ I2I3 = I1 ∩ I2 ∩ I3 = I1 I2 I3
|
が成り立つことがわかる。この議論を繰り返すことにより
∩i=1k Ii = I1 I2 ⋯ Ikが得られる。
Φが単射であることは、自然な射影
R → R/I1×⋯×R/Ik, a ↦ (a(mod I1),⋯,a(mod Ik)の核が
∩i=1kIiであることから、準同型定理を適用することによってわかる。したがって全射であることを示せばよい。まず、
k=2のときを考える。
1=b1+b2, b1∈I1, b2∈I2とする。任意の
a1,a2∈Rに対して、
c=a2b1+a1b2とおくと
| | | a2b1 + a1(1-b1) = a1 + (a2 - a1)b1 ≡ a1 (mod I1) |
|
| | | a2(1-b2) + a1b2 = a2 + (a1 - a2)b2 ≡ a2 (mod I2) |
|
となり、
Φ(c)=(a1(mod I1),a2(mod I2))であることがわかる。
k=3の場合は
I1と
I2I3が互いに素であることから、
| R/I1 I2 I3 ≅ R/I1 × R/I2 I3 ≅ R/I1 × R/I2 × R/I3
|
が成り立ち、この議論を繰り返すことにより、
R/I1⋯Ik≅R/I1×⋯×R/Ikが得られる。■
a ≈ p1e1⋯pkekを単項イデアル整域
Rにおける元
aの素元分解とすれば、
| R/(a) ≅ R/(p1e1) × ⋯ × R/(pkek)
|
[
2] ファン・デル・ヴェルデン, 現代代数学〈1〉, 商工出版社, 1959
数 学
剰余環 じょうよかん, residue ring
準同型写像 じゅんどうけいしゃぞう, homomorphism map
同型写像 どうけいしゃぞう, isomorphism map
同型 どうけい, isomorphic
核 かく, kernel
包含写像 ほうがんしゃぞう, inclusion mapping
集合Aとその部分集合Pが与えられたときに、a∈Pに対してa∈Aを対応させる写像。
標数 ひょうすう, characteristic