一次合同式
著者:梅谷 武
語句:ガーナー,秦九韶,合同式,連立一次合同式,孫子算経,中国の剰余定理,数書九章,大衍求一術
一次合同式について述べる。
作成:2006-06-10
更新:2021-03-17
5.2 一次合同式
 mを正の整数、f(X1,⋯,Xn)を整係数k次多項式であってk次の項の係数akが法mで0と合同でないとき、すなわちak≢0(mod m)で あるときに
f(X1,⋯,Xn) ≡ 0 (mod m)
をn元k次合同式ごうどうしき, congruenceといいます。f(α1,⋯,αn)=0なる整数の組(α1,⋯,αn)をこの合同式の解といい、解を求めることを合同式を解くといいます。合同式においては元の多項式の係数を法mで合同な数に置き換えてもかまいません。次節において剰余環ℤ/mℤを考えますが、合同式はℤ/mℤ上の代数方程式に他なりません。
 n元一次合同式
a1 X1 + ⋯ + an Xn ≡ b (mod m)
は、n+1元一次不定方程式
a1 X1 + ⋯ + an Xn － m Xn+1 = b
と同等ですから、一次不定方程式の解法で解くことができます。第2章で得た二元一次不定方程式に関する結果を一次合同式に当てはめてみましょう。

命題5.2.3

 正の整数mと0でない整数a,bについて、一次合同式
aX ≡ b (mod m)
は、d=(a,m)としたときにd|bのときにmを法としてd個の解を持つ。

証明

aX － mY = b
に命題2.6.17を適用すると、d=(a,m),a=a'd,－m=－m'd,b=b'dとし、aX － mY = dの特殊解を(x0,y0)としたときに一般解は
{ (b'x0 + m't, b'y0+a't) | t ∈ℤ }
と表わされる。この一般解のX成分を法mで考えると
(b'x0 + m't1) － (b'x0 + m't2) = m'(t1 － t2) ≡ 0 (mod m)
となるのはt1 ≡ t2 (mod d)のときであることがわかる。よって合同式の解は
{ b'x0 + m't | t = 0,1,⋯,d－1 }
となる。■

系5.2.5

 正の整数mと0でない整数a,bについて、一次合同式
aX ≡ b (mod m)
は、(a,m)=1のときにmを法として一意的な解を持つ。

連立一次合同式

 3世紀頃の中国の数学書『孫子算経』に「三つずつ数えると二が余り、五つずつ数えると三が余り、七つずつ数えると二が余るような数はいくつであるか。」という問題とその解法が書かれています。
 これを合同式で表すと、
lc96
X ≡ 2 (mod 3)
X ≡ 3 (mod 5)
X ≡ 2 (mod 7)
という連立一次合同式になります。これは次のように順番に解いていくことができます。まずX≡2(mod 3)の解は{2 + 3s | s ∈ℤ}と表すことができます。これを二番目の合同式X≡3(mod 5)に代入すると、3s≡1(mod 5)となりますが、これは(3,5)=1であることからs0をその特殊解として{s0 + 5 t | t ∈ℤ}という解を持ちます。これを最初の解に代入することで、
{ 2 + 3s0 + 15t | t ∈ℤ }
が得られます。これは
lc48
X ≡ 2 (mod 3)
X ≡ 3 (mod 5)
の解になっています。同じように三番目の合同式X≡2(mod 7)にこれを代入すると15t≡－3s0 (mod 7)となり、(15,7)=1よりt0をその特殊解として{t0 + 7 u | u ∈ℤ}という解を得ます。これを二番目の解に代入して最終的な解
{ 2 + 3s0 + 15t0 + 105 u | u ∈ℤ }
を求めることができます。この解は2+3s0+15t0(mod 105)と書け、s0=2,t0=1を代入すると23(mod 105)になります。
 このように一次合同式を順番に解いていけばいいのですが、『孫子算経』ではもっと簡単に次のような方法で解いています。5⋅7,3⋅7,3⋅5の倍数で法3,5,7で1となるような三つの数70,21,15を考え、
lc96
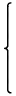70 ≡ 0 (mod 5⋅7), 70 ≡ 1 (mod 3)
21 ≡ 0 (mod 3⋅7), 21 ≡ 1 (mod 5)
15 ≡ 0 (mod 3⋅5), 15 ≡ 1 (mod 7)
それらと合同式の余りを使って
233 = 2⋅70 + 3⋅21 + 5⋅15
という数を計算し、これから3⋅5⋅7=105を引けるだけ引いて得られる数23が105を法とする解となっているというものです。
 この解法を一般化すると中国の剰余定理ちゅうごくのじょうよていり, Cheinese remainder theoremあるいは中国では孫子の剰余定理と呼ばれている次の定理になります。

定理5.2.10 中国の剰余定理I

 m1,m2,⋯,mkを互いに素であるような正の整数としたときに、任意の整数a1,a2,⋯,akについて、連立一次合同式
(5.1)
lc144
X ≡ a1 (mod m1)
X ≡ a2 (mod m2)
⋯⋯
X ≡ ak (mod mk)
はM = m1 m2 ⋯ mkを法として一意的な解を持つ。

証明

 Mi=M/mi, i=1,⋯,kと置き、(Mi,mi)=1より存在が保証されている
Mi ti ≡ 1 (mod mi)
の特殊解をtiとする。このとき
a ≡ a1 M1 t1 + a2 M2 t2 + ⋯ + ak Mk tk (mod M)
が求める解になっている。これがMを法として一意的であることは、もう一つ別の解bがあったとすると、a ≡ b (mod mi),i=1,⋯,kよりa ≡ b (mod M)となることからわかる。■
 上の証明の算法は構成的ですが、実際にはガーナーGarner, Harvey Louisによって効率よく計算できるように工夫された方法がよく使われます。

算法5.2.13 ガーナー法

 中国の剰余定理における解を求める。
Step 1.  拡張ユークリッド算法により、
micij≡1(mod mj),  1≦i＜j ≦ k
なるcijを計算する。
Step 2.  vr, r=1,⋯,kを次のように計算する。
v1 = a1 % m1
v2 = (a2 － v1)c12 % m2
⋯⋯
vr = (⋯((ar－v1)c1r－v2)c2r－⋯－vr)c(r－1)r % mr
⋯⋯
Step 3.  解a(0≦a＜M)を次のように計算する。
a = vk mk－1 ⋯ m1 + ⋯ + v3 m2 m1 + v2 m1 + v1

証明

vr mr－1 ⋯ m1
≡
mr－1 ⋯ m1 (⋯((ar－v1)c1r－v2)c2r－⋯－vr)c(r－1)r (mod mr)
≡
mr－2 ⋯ m1 (⋯((ar－v1)c1r－v2)c2r－⋯－vr)c(r－2)r
－ vr－1 mr－2 ⋯ m1 (mod mr)
⋯⋯
≡
ar － v1 － v2 m1 － v3 m2 m1 － ⋯ － vr－1 mr－2 ⋯ m1 (mod mr)
より解であることがわかる。0≦a＜Mは0≦vrmr－1⋯m1＜mrmr－1⋯m1より。■
 ガーナー法は、法の組を固定して巨大な数を分割して計算する目的で使われることが多く、その場合cijは定数として数表化することができます。孫子算経の方法とガーナー法で実際に連立一次合同式を解いてみましょう。

sample5.2.4.py

def gcd_ext( a, b, val = [ 0, 0 ] ):
  if ( a == 0 ) or ( b == 0 ):
    return 0
  s = a; t = b; u = 1; v = 0
  while t != 0:
    q = s / t; r = s % t
    s = t; t = r
    temp = v; v = u - q * v; u = temp
  val[0] = u
  val[1] = ( s - u * a ) / b
  if s < 0:
    val[0] = -val[0]
    val[1] = -val[1]
    return -s
  else:
    return s
 
Mods = [ 1279, 2203, 2281, 3217, 4253 ]
Rems = [ 102, 235, 495, 627, 318 ]
print 'Modulos:', Mods
print 'Remainders:', Rems
val = [ 0, 0 ]
 
# Chinese
M = 1
for m in Mods: M *= m
a = 0
for i in range( len(Mods) ):
  Mi = M / Mods[i]; 
  gcd_ext( Mi, -Mods[i], val )
  a += Rems[i] * val[0] * Mi
a = a % M
print a, 'mod', M
 
# Garner
c = []
for i in range( len(Mods) ):
  c.append( range( len(Mods) ) )
for r in range( 1, len(Mods), 1 ):
  for i in range( r ):
    gcd_ext( Mods[i], -Mods[r], val )
    c[i][r] = val[0]
 
v = [ Rems[0] % Mods[0] ]
for r in range( 1, len(Mods), 1 ):
  tmp = Rems[r]
  for i in range( r ):
    tmp = ( tmp - v[i] ) * c[i][r]
  v.append( tmp % Mods[r] )
 
a = 0
for r in range( len(Mods) ):
  tmp = v[r]
  for i in range( r ):
    tmp *= Mods[i]
  a += tmp
print a, 'mod', M

sample5.2.4.pyの実行結果

Modulos: [1279, 2203, 2281, 3217, 4253]
Remainders: [102, 235, 495, 627, 318]
83992724037350681 mod 87933988142984297
83992724037350681 mod 87933988142984297

sample5.2.4.rb

def gcd_ext(a, b, val = [0, 0])
  if ( a == 0 ) or ( b == 0 )
    return 0
  end
  s = a; t = b; u = 1; v = 0
  while t != 0
    q = s / t; r = s % t
    s = t; t = r
    temp = v; v = u - q * v; u = temp
  end
  val[0] = u
  val[1] = (s - u * a) / b
  if s < 0
    val[0] = -val[0]
    val[1] = -val[1]
    return -s
  else
    return s
  end
end
 
mods = [1279, 2203, 2281, 3217, 4253]
rems = [102, 235, 495, 627, 318]
print "Modulos: "; p mods
print "Remainders: "; p rems
val = [0, 0]
 
# Chinese
m = 1
for s in mods
  m *= s
end
a = 0
for i in 0...mods.length
  mi = m / mods[i]
  gcd_ext(mi, -mods[i], val)
  a += rems[i] * val[0] * mi
end
a = a % m
print a, " mod ", m, "\n"
 
# Garner
c = Array.new(mods.length) { Array.new(mods.length) { |i| i } }
for r in 1...mods.length
  for i in 0...r
    gcd_ext(mods[i], -mods[r], val)
    c[i][r] = val[0]
  end
end
 
v = [rems[0] % mods[0]]
for r in 1...mods.length
  tmp = rems[r]
  for i in 0...r
    tmp = ( tmp - v[i] ) * c[i][r]
  end
  v.push(tmp % mods[r])
end
 
a = 0
for r in 0...mods.length
  tmp = v[r]
  for i in 0...r
    tmp *= mods[i]
  end
  a += tmp
end
print a, " mod ", m, "\n"

sample5.2.4.rbの実行結果

Modulos: [1279, 2203, 2281, 3217, 4253]
Remainders: [102, 235, 495, 627, 318]
83992724037350681 mod 87933988142984297
83992724037350681 mod 87933988142984297

秦九韶の大衍求一術

 『孫子算経』においては法が互いに素の場合だけを考えていましたが、13世紀南宋の秦九韶Shin, Kyusho, 1202-1261は1247年の著書『数書九章』において、aX≡b(mod m), (a,m)=1の形の一次合同式をユークリッド算法とほぼ同等な方法を使って解き、大衍求一術だいえんきゅういつじゅつと名付けられた、法が互いに素でない場合の連立一次合同式の解法を与えています。『数書九章』には素因数分解の概念は表れていませんが、実質的には素因数分解を使った解法とほぼ同じものになっています。ここではこれをすでに学んでいる記号や概念を使って再現してみましょう。
 まず、これまでの議論を使って法が互いに素ではないときはどのようになるかを考えます。d=(m1,m2)が1とは限らないときに
lc48
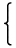X ≡ a1 (mod m1), m1 = m1'd
X ≡ a2 (mod m2), m2 = m2'd
という連立一次合同式を解いてみます。X≡a1(mod m1)の解は{a1 + m1 s | s ∈ℤ}と表すことができます。これを二番目の合同式X≡a2(mod m2)に代入すると、 m1s≡a2－a1(mod m2)となりますが、これはd|a2－a1のときに解くことができて、s0をその特殊解として{s0 + m2' t | t ∈ℤ}という解を持ちます。これを最初の解に代入することで、
{ a1 + m1s0 + m1 m2' t | t ∈ℤ }
求める解が得られます。これを一般化すると次の命題が得られます。

命題5.2.22

 m1,m2,⋯,mkを任意の正の整数としたときに、連立一次合同式
lc144
X ≡ a1 (mod m1)
X ≡ a2 (mod m2)
⋯⋯
X ≡ ak (mod mk)
は
ai ≡ aj (mod gcd(mi,mj)), 1 ≦ i,j ≦ k, i ≠ j
が成り立つときにm1,m2,⋯,mkの最小公倍数を法として一意的な解を持つ。

証明

 演習とする。■
 連立一次合同式のもっとも一般的な形は
lc144
a1X ≡ b1 (mod m1)
a2X ≡ b2 (mod m2)
⋯⋯
akX ≡ bk (mod mk)
というものですが、これは命題5.2.3によって命題5.2.22へ帰着させることができます。
 命題5.2.22の形の連立一次合同式が与えられたとして、その一般的な解法を考えます。まず、各法を素因数分解し、対応する合同式をそれによって分解します。mi = p1e1 ⋯ prerと素因数分解したとすると、X≡ai(mod mi)は
lc144
X ≡ ai (mod p1e1)
X ≡ ai (mod p2e2)
⋯⋯
X ≡ ai (mod prer)
と分解することができます。中国の剰余定理により、これは元の合同式と同等です。これをi=1,⋯,kに対して行って、そのすべての素因数の集合Pの各元pについてその冪が最大となる合同式だけを集めて、新たな連立一次合同式
X ≡ ap (mod pep), p∈P
を作成します。これはm1,m2,⋯,mkの最小公倍数を法として一意的な解を持ちますが、それが必ずしも元の連立合同式の解になるとは限りません。したがってこの解が元の連立合同式を満足すれば解となり、そうでない場合は、元の連立合同式は解けないということになります。

例題5.2.26

lc96
X ≡ 30 (mod 120)
X ≡ 20 (mod 110)
X ≡ 30 (mod 100)
 これは120=23⋅3⋅5, 110=2⋅5⋅11, 100=22⋅52より
lc144
X ≡ 30 (mod 8)
X ≡ 30 (mod 3)
X ≡ 20 (mod 11)
X ≡ 30 (mod 25)
に還元されます。これを sample5.2.4.py を使って解くと1230(mod 6600)が得られます。これを元の合同式に代入すると
lc96
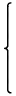1200 = 120⋅10 ≡ 0 (mod 120)
1210 = 110⋅11 ≡ 0 (mod 110)
1200 = 100⋅12 ≡ 0 (mod 100)
となり、1230(mod 6600)が元の合同式の解であることがわかります。

参考文献

[1] 高木 貞治, 初等整数論講義 第2版, 共立出版, 1971
img
 
 
[2] 遠山 啓, 初等整数論, 日本評論社, 1972
img
 
 
[3] 木田 祐司, 牧野 潔夫, UBASICによるコンピュータ整数論, 日本評論社, 1994
[4] 木田 祐司, 講座 数学の考え方〈16〉初等整数論, 朝倉書店, 2001
img
 
 
[5] D.E.Knuth（中川圭介訳）, 準数値算法―算術演算, サイエンス社, 1986
img
 
 
[6] D.E.Knuth（有沢誠他訳）, The Art of Computer Programming (2) 日本語版 Seminumerical algorithms, アスキー, 2004
img
 
 
[7] 伊東 俊太郎, 数学の歴史(2) 中世の数学, 共立出版, 1987
img
 
 
人　　物
ガーナー Garner, Harvey Louis
クヌースによればこの算法は1958年に提出されており、いくつかのバリエーションをもっている。
秦九韶 Shin, Kyusho, 1202-1261
南宋時代の数学者。
 
数　　学
合同式 ごうどうしき, congruence
中国の剰余定理 ちゅうごくのじょうよていり, Cheinese remainder theorem
大衍求一術 だいえんきゅういつじゅつ
 
Published by SANENSYA Co.,Ltd.