ベルヌーイ数の母関数
著者:梅谷 武
語句:母関数,指数型母関数
ベルヌーイ数の母関数について述べる。
作成:2006-05-27
更新:2021-03-17
形式的な指数関数
eXを
によって定義します。これも関数ではなく形式的冪級数ですが、形式的冪級数としての微分に関して関数としての微分と同様に
が成り立ちます。
証明
とすると
であるが、これはパスカルの算術三角形の指数
iの底辺の交代和であることから
| = δ0i = | 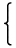 | | |
|
となる。この詳細は演習とする。■
次の定理はベルヌーイ数を特徴付けるものです。
ℚ((X))においてベルヌーイ数の指数型母関数と指数関数に関する次の式が成り立つ。
証明
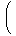 | | 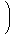 | (eX - 1) |
| | |
| | |
ここでベルヌーイ数の漸化式
を代入すれば、
となる。■
今後、ベルヌーイ数の指数型母関数を単にベルヌーイ数の母関数と呼び、それを
B(X)と書くことにします。
これに
-Xを代入すると
ですから、
が成り立ちます。これは形式的冪級数としての等式
ですから、
i=1のとき
B1 = 1/2、
i=2n+1(n ≧ 1)のとき
B2n+1=0であることがわかります。
1より大きい奇数
iに対応するベルヌーイ数
Biは
0である。
ベルヌーイ数の母関数の奇数次の項は一次の項を除いて
0であることがわかりました。
この一次の項を除いたものを
E(X)と置きます。
これを微分すると
| | |
| | | - | | + | | - | | | 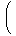 | | 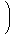 | |
|
この両辺に
Xを掛けて整理すると
これより、
が得られますが、これを形式的冪級数としてあらわに書き下すと
となります。
i>1で両辺の係数を比較すると
右辺の和において
j=0,iのとき
B2iになるのでそれを左辺に移項し、整理すること
によって、オイラーが発見したベルヌーイ数の漸化式が得られます。
この公式を利用するとベルヌーイ数の符号を知ることができます。
i≧1が奇数のとき
B2iは正であり、偶数のとき負となる。
証明
オイラーの漸化式の両辺に
(-1)i-1を掛けると
| (-1)i-1B2i = | | i-1
∑
j=1 | | (-1)j-1B2j(-1)i-j-1B2(i-j) |
|
|
|
となる。これにより数学的帰納法で
(-1)i-1B2i>0を証明する。
i=1のときは
B2 = 1/6>0である。
i-1まで正しいと仮定すると右辺は正であるから、左辺も正となる。■
数 学
母関数 ぼかんすう, generating function
指数型母関数 しすうがたぼかんすう, exponential generating function

