スターリング数と冪和公式

著者:梅谷武
語句:昇階乗,降階乗,第1種スターリング数,第2種スターリング数

スターリング数と冪和公式について述べる。

作成:2006-05-26
更新:2021-03-17

4.4 スターリング数と冪和公式

4.2節では三角数や四面体数等の重和が算術三角形を利用することで計算できることを示しました。ここでは、同じように冪和が算術三角形を利用することで計算できることを示します。

これまで階乗という言葉を正の整数kについてk! = 1⋅2⋅3⋅⋯⋅kなるものとして使ってきましたが、ここでその概念を拡張します。正の整数nに対してk次の昇階乗しょうかいじょう, rising factorialを

(4.1)

n^k = n(n+1)⋯(n+k－1) (k個の積)

k次の降階乗こうかいじょう, falling factorialを

(4.2)

n^k = n(n－1)⋯(n－k+1) (k個の積)

と定義します。0に対しては便宜上n⁰ = n⁰ = 1と定義します。

同じように有理数体上の多項式環ℚ[X]において、正の整数nに対して不定元Xに対するk次の昇階乗を

(4.3)

Xⁿ = X(X+1)⋯(X+n－1) (n個の積)

n次の降階乗を

(4.4)

Xⁿ = X(X－1)⋯(X－n+1) (n個の積)

と定義します。0に対しては便宜上X⁰ = X⁰ = 1と定義します。

算術三角形を階乗公式によって階乗で表現してみましょう。

図4.4.5 階乗で表現した算術三角形

重和を考えるときは算術三角形の横方向の数列を考えましたが、今度は縦方向の数列に着目してみます。例えば第3列(C(i,3))_{i ∈ℕ}は、

(i+1)(i+2)(i+3)

_{i ∈ℕ}

という数列になっています。この数列の第n項までの和は(P3)により

n－1
∑
i=0

(i+1)(i+2)(i+3)

n(n+1)(n+2)(n+3)

となりますから、

n－1
∑
i=0

(i+1)(i+2)(i+3)

n(n+1)(n+2)(n+3)

が得られます。この式は立方数の和の公式

P₃(n) =

n
∑
i=1

i³

n²(n+1)²

と似ています。これは冪乗i³と階乗(i+1)(i+2)(i+3)が近い関係にあることによります。階乗の和の公式がすでにわかっていますので、冪乗と階乗との関係がわかれば、それを使って冪和の公式が得られそうです。そこで、まず冪乗と階乗の関係について考えていくことにしましょう。

Xⁿはn次の多項式ですから、これを展開したときのk次の係数を

[

n
k

]

と書くことにすると

(4.5)

Xⁿ =

n
∑
k=0

[

n
k

]

X^k

と展開することができます。これにより自然数n,k(n ≧ k ≧ 0)に対して数

[

n
k

]

を定義することができます。これを第1種スターリング数だい1しゅすたーりんぐすう, Stirling cycle numberといいます。第1種スターリング数は負にはならず、

(4.6)

[

n
0

]

= 0,

[

n
n

]

= 1

であることはすぐにわかります。また、XⁿとXⁿの展開式における係数は符号が異なるだけで

(4.7)

Xⁿ =

n
∑
k=0

(－1)^n－k

[

n
k

]

X^k

と書けることもわかります。第1種スターリング数は組み合わせと同じように加法公式が存在します。

補題4.4.8 第1種スターリング数の加法公式

任意の自然数n,k(n＞k＞0)に対して次の式が成り立つ。

(4.8)

[

n
k－1

]

+ n

[

n
k

]

[

n+1
k

]

証明

Xⁿ⁺¹ = (X + n)Xⁿ = X ⋅ Xⁿ + n ⋅ Xⁿより、

Xⁿ⁺¹

n+1
∑
k=0

[

n+1
k

]

X^k

n+1
∑
k=1

[

n
k－1

]

X^k

+ n

n
∑
k=0

[

n
k

]

X^k

となりn＞k＞0なるkについて係数を比較することによってわかる。■

この加法公式を使って、第1種スターリング数の三角形を作ってみましょう。作り方は三角形の細胞をパスカルの三角形と同じくC(i,j)と書くことにすれば、

C(i,j) =

[

i+j
j

]

とします。言い換えれば、パスカルの算術三角形における

(

n
k

)

を

[

n
k

]

で置き換えたものです。まず、

[

0
0

]

= 1

とし、n＞0に対して

[

n
0

]

= 0,

[

n
n

]

= 1

とすることによって第0行と第0列が埋まります。次に加法公式によって上の行の左から順番に

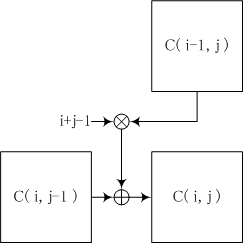
C(i,j) = C(i,j－1) + (i+j－1)C(i－1,j)

図4.4.11 生成規則

によって細胞を埋めていき、行末になったら下の行の左から同じように埋めていくという手順ですべての細胞を埋めることができます。

図4.4.13 第1種スターリング数の三角形

第1種スターリング数の三角形だい1しゅすたーりんぐすうのさんかくけいを一見して気が付くのは第1行が三角数になっていることと第1列が

C(i,1) =

[

i+1
1

]

= i!

と狭義の階乗になっていることでしょう。さらに底辺の和は次のようにちょうど狭義の階乗になっています。

n
∑
k=0

[

n
k

]

= n!

これは第1種スターリング数を組み合わせ論的に解釈することによって比較的容易に証明することができますが、これについては章末の研究で詳しく考えることにします。

このようにしてできあがった第1種スターリング数の三角形が正しいかどうかを、多項式を展開した係数と比較することによって確認してみましょう。

sample4.4.1.py

from Poly1 import *
 
def RisingFactorial( n ):
  if n == 0: return Poly1( [1] )
  a = b = Poly1( [0,1] )
  for i in range( n - 1 ):
    b = b + Poly1( [1] )
    a = a * b
  return a
 
def FallingFactorial( n ):
  if n == 0: return Poly1( [1] )
  a = b = Poly1( [0,1] )
  for i in range( n - 1 ):
    b = b - Poly1( [1] )
    a = a * b
  return a
 
for i in range( 10 ):
  print "i = ", i
  print RisingFactorial( i )
  print FallingFactorial( i )

sample4.4.1.pyの実行結果

i =  0
1
1
i =  1
X
X
i =  2
X^2 + X
X^2 - X
i =  3
X^3 + 3X^2 + 2X
X^3 - 3X^2 + 2X
i =  4
X^4 + 6X^3 + 11X^2 + 6X
X^4 - 6X^3 + 11X^2 - 6X
i =  5
X^5 + 10X^4 + 35X^3 + 50X^2 + 24X
X^5 - 10X^4 + 35X^3 - 50X^2 + 24X
i =  6
X^6 + 15X^5 + 85X^4 + 225X^3 + 274X^2 + 120X
X^6 - 15X^5 + 85X^4 - 225X^3 + 274X^2 - 120X
i =  7
X^7 + 21X^6 + 175X^5 + 735X^4 + 1624X^3 + 1764X^2 + 720X
X^7 - 21X^6 + 175X^5 - 735X^4 + 1624X^3 - 1764X^2 + 720X
i =  8
X^8 + 28X^7 + 322X^6 + 1960X^5 + 6769X^4 + 13132X^3 + 13068X^2 + 5040X
X^8 - 28X^7 + 322X^6 - 1960X^5 + 6769X^4 - 13132X^3 + 13068X^2 - 5040X
i =  9
X^9 + 36X^8 + 546X^7 + 4536X^6 + 22449X^5 + 67284X^4 + 118124X^3 + 109584X^2 + 40320X
X^9 - 36X^8 + 546X^7 - 4536X^6 + 22449X^5 - 67284X^4 + 118124X^3 - 109584X^2 + 40320X

sample4.4.1.rb

require 'mathn'
require './poly1'
 
def RisingFactorial(n)
  if n == 0
    return Poly1([1])
  end
  a = b = Poly1([0,1])
  for i in 0...(n-1)
    b = b + Poly1([1])
    a = a * b
  end
  return a
end
 
def FallingFactorial(n)
  if n == 0
    return Poly1([1])
  end
  a = b = Poly1([0,1])
  for i in 0...(n-1)
    b = b - Poly1([1])
    a = a * b
  end
  return a
end
 
for i in 0...10
  print "i = ", i, "\n"
  print RisingFactorial(i), "\n"
  print FallingFactorial(i), "\n"
end

sample4.4.1.rbの実行結果

i =  0
1
1
i =  1
X
X
i =  2
X^2 + X
X^2 - X
i =  3
X^3 + 3X^2 + 2X
X^3 - 3X^2 + 2X
i =  4
X^4 + 6X^3 + 11X^2 + 6X
X^4 - 6X^3 + 11X^2 - 6X
i =  5
X^5 + 10X^4 + 35X^3 + 50X^2 + 24X
X^5 - 10X^4 + 35X^3 - 50X^2 + 24X
i =  6
X^6 + 15X^5 + 85X^4 + 225X^3 + 274X^2 + 120X
X^6 - 15X^5 + 85X^4 - 225X^3 + 274X^2 - 120X
i =  7
X^7 + 21X^6 + 175X^5 + 735X^4 + 1624X^3 + 1764X^2 + 720X
X^7 - 21X^6 + 175X^5 - 735X^4 + 1624X^3 - 1764X^2 + 720X
i =  8
X^8 + 28X^7 + 322X^6 + 1960X^5 + 6769X^4 + 13132X^3 + 13068X^2 + 5040X
X^8 - 28X^7 + 322X^6 - 1960X^5 + 6769X^4 - 13132X^3 + 13068X^2 - 5040X
i =  9
X^9 + 36X^8 + 546X^7 + 4536X^6 + 22449X^5 + 67284X^4 + 118124X^3 + 109584X^2 + 40320X
X^9 - 36X^8 + 546X^7 - 4536X^6 + 22449X^5 - 67284X^4 + 118124X^3 - 109584X^2 + 40320X

第1種スターリング数によって、階乗を冪乗の多項式として表わすことができました。今度は逆に冪乗を階乗の多項式として表わすことを考えてみましょう。冪乗は

X² = X(X－1) + X, X³ = X(X－1)(X－2) + 3X(X－1) + X

というように降階乗の多項式で表わすことができます。これを一般化して

(4.9)

Xⁿ =

n
∑
k=0

{

n
k

}

X^k

により自然数n,k(n≧k≧0)に対して数

{

n
k

}

を定義します。これを第2種スターリング数だい2しゅすたーりんぐすう, Stirling subset numberといいます。第2種スターリング数が負にはならず、

(4.10)

{

n
0

}

= 0,

{

n
n

}

= 1

であることはすぐにわかります。第2種スターリング数は次の加法公式を満たします。

補題4.4.21 第2種スターリング数の加法公式

任意の自然数n,k(n＞k＞0)に対して次の式が成り立つ。

(4.11)

{

n
k－1

}

+ k

{

n
k

}

{

n+1
k

}

証明

まず、{X^k | k∈ℕ}がℚ[X]において ℚ上線形独立であることを注意しておく。すなわち、

∑
k

a_k X^k

= 0

ならばすべてのa_kは0である。

X^k+1 = (X － k)X^k

より、

X ⋅ X^k = X^k+1 + k ⋅ X^k

であるから、

Xⁿ⁺¹

n+1
∑
k=0

{

n+1
k

}

X^k

n+1
∑
k=1

{

n
k－1

}

X^k

+ k

n
∑
k=0

{

n
k

}

X^k

となりn＞k＞0なるkについて係数を比較することによってわかる。■

この加法公式を使って第2種スターリング数の三角形を作ってみましょう。作り方は第1種スターリング数の三角形と同様に

C(i,j) =

{

i+j
j

}

とします。

{

0
0

}

n＞0に対して

{

n
0

}

= 0,

{

n
n

}

= 1

とし、加法公式

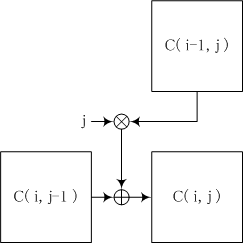
C(i,j) = C(i,j－1) + j C(i－1,j)

図4.4.24 生成規則

によって細胞を埋めていきます。

図4.4.26 第2種スターリング数の三角形

第2種スターリング数の三角形においても第1行が三角数になっています。また、第2列が

{

n
2

}

= 2^n－1 － 1, n ≧ 2

となっています。これも組み合わせ論的に解釈することによって容易に証明できますので、章末の研究で考えることにします。

冪乗の昇階乗に関する多項式は符号を考慮するだけで得られます。

(4.12)

Xⁿ =

n
∑
k=0

(－1)^n－k

{

n
k

}

X^k

第2種スターリング数の三角形が正しいかどうかを確認してみましょう。

sample4.4.2.py

from Poly1 import *
 
def RisingFactorial( n ):
  if n == 0: return Poly1( [1] )
  a = b = Poly1( [0,1] )
  for i in range( n - 1 ):
    b = b + Poly1( [1] )
    a = a * b
  return a
 
def FallingFactorial( n ):
  if n == 0: return Poly1( [1] )
  a = b = Poly1( [0,1] )
  for i in range( n - 1 ):
    b = b - Poly1( [1] )
    a = a * b
  return a
 
stir2 = [ [1,1],\
          [1,3,1],\
          [1,6,7,1],\
          [1,10,25,15,1],\
          [1,15,65,90,31,1],\
          [1,21,140,350,301,63,1],\
          [1,28,266,1050,1701,966,127,1],\
          [1,36,462,2646,6951,7770,3025,255,1] ]
 
for n in range( 2, 10, 1 ):
  coef = stir2[n-2]
  i = n; a = b = Poly1([0])
  sign = p = Poly1([1]); m = Poly1([-1])
  for k in coef:
    a += Poly1([k])*FallingFactorial( i )
    b += sign * Poly1([k])*RisingFactorial( i )
    if sign == p: sign = m
    else: sign = p
    i = i - 1
  print "X^%d = " % n, a, ", ", b

sample4.4.2.pyの実行結果

X^2 =  X^2 ,  X^2
X^3 =  X^3 ,  X^3
X^4 =  X^4 ,  X^4
X^5 =  X^5 ,  X^5
X^6 =  X^6 ,  X^6
X^7 =  X^7 ,  X^7
X^8 =  X^8 ,  X^8
X^9 =  X^9 ,  X^9

sample4.4.2.rb

require 'mathn'
require './poly1'
 
def RisingFactorial(n)
  if n == 0
    return Poly1([1])
  end
  a = b = Poly1([0,1])
  for i in 0...(n-1)
    b = b + Poly1([1])
    a = a * b
  end
  return a
end
 
def FallingFactorial(n)
  if n == 0
    return Poly1([1])
  end
  a = b = Poly1([0,1])
  for i in 0...(n-1)
    b = b - Poly1([1])
    a = a * b
  end
  return a
end
 
stir2 = [ [1,1],
          [1,3,1],
          [1,6,7,1],
          [1,10,25,15,1],
          [1,15,65,90,31,1],
          [1,21,140,350,301,63,1],
          [1,28,266,1050,1701,966,127,1],
          [1,36,462,2646,6951,7770,3025,255,1] ]
 
for n in 2...10
  coef = stir2[n-2]
  i = n; a = b = Poly1([0])
  sign = p = Poly1([1]); m = Poly1([-1])
  for k in coef
    a += Poly1([k]) * FallingFactorial(i)
    b += sign * Poly1([k]) * RisingFactorial(i)
    if sign == p
      sign = m
    else
      sign = p
    end
    i = i - 1
  end
  printf "X^%d = %s, %s\n", n, a, b
end

sample4.4.2.rbの実行結果

X^2 =  X^2 ,  X^2
X^3 =  X^3 ,  X^3
X^4 =  X^4 ,  X^4
X^5 =  X^5 ,  X^5
X^6 =  X^6 ,  X^6
X^7 =  X^7 ,  X^7
X^8 =  X^8 ,  X^8
X^9 =  X^9 ,  X^9

さて、ここまでの準備によってP_k(n)をnの多項式として書き下すことができるようになりました。まず、冪乗を第2種スターリング数によって昇階乗に書き換えます。

P_k(n)

n
∑
i=1

i^k

n
∑
i=1

k
∑
j=0

(－1)^k－j

{

k
j

}

i^j

昇階乗の指数が同じものの和をまとめ、パスカルの帰結(P3)を適用します。

P_k(n)

k
∑
j=0

(－1)^k－j

{

k
j

}

n－1
∑
i=0

i^j

k
∑
j=0

(－1)^k－j

j+1

{

k
j

}

n^j+1

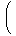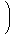この昇階乗を第1種スターリング数によって冪乗に書き換えて、同じ次数の単項式の和として整理します。

P_k(n)

k
∑
j=0

(－1)^k－j

j+1

{

k
j

}

j+1
∑
t=0

[

j+1
t

]

n^t

k+1
∑
t=0

k
∑
j=0

(－1)^k－j

j+1

{

k
j

}

[

j+1
t

]

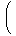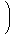n^t

ここでt＞j+1のとき

[

j+1
t

]

= 0

としていることに注意してください。これでP_k(n)をnの多項式として書くことができました。

[

j+1
0

]

= 0

であることを考慮してこれを命題としておきましょう。

命題4.4.35 スターリング数による冪和公式

自然数列のk次の冪和は次のように表すことができる。

(4.13)

P_k(n) =

k+1
∑
t=1

k
∑
j=t－1

(－1)^k－j

j+1

{

k
j

}

[

j+1
t

]

n^t

, k∈ℕ

これからベルヌーイ数をスターリング数を使って求める公式が導かれます。

系4.4.37 ベルヌーイ数の計算公式I

(4.14)

B_k = (－1)^k

k
∑
j=0

(－1)^jj!

j+1

{

k
j

}

, k∈ℕ

証明

ベルヌーイ数B_kはP_k(X)の一次の係数であるから、

B_k =

k
∑
j=0

(－1)^k－j

j+1

{

k
j

}

[

j+1
1

]

この式に

[

j+1
1

]

= j!

を代入する。■

次にスターリング数による冪和公式があっているかどうかを確かめてみますが、計算の都合上、

(4.15)

[

n
k

]

{

n
k

}

= 0, k＞n≧0

と定義することにします。

sample4.4.3.py

from Poly1 import *
 
# calculate tables
tr1 = []
tr2 = []
for i in range( 10 ):
  tr1.append( range( 0, 10, 1 ) )
  tr2.append( range( 0, 10, 1 ) )
for j in range( 10 ):
  tr1[0][j] = tr2[0][j] = 1
for i in range( 1, 10, 1 ):
  for j in range( 1, 10, 1 ):
    tr1[i][j] = tr1[i][j-1] + (i+j-1) * tr1[i-1][j]
    tr2[i][j] = tr2[i][j-1] +       j * tr2[i-1][j]
 
def s( n, k ):
  if not isinstance( n, int ): raise TypeError
  if not isinstance( k, int ): raise TypeError
  if ( k < 0 ) or ( n < 0 ): raise TypeError
  if ( k > 9 ) or ( n > 9 ): raise TypeError
  if ( k > n ): return 0
  else:
    if ( n == 0 ) and ( k == 0 ): return 1
    elif n == k: return 1
    elif k == 0: return 0
    else:        return tr1[n-k][k]
 
def S( n, k ):
  if not isinstance( n, int ): raise TypeError
  if not isinstance( k, int ): raise TypeError
  if ( k < 0 ) or ( n < 0 ): raise TypeError
  if ( k > 9 ) or ( n > 9 ): raise TypeError
  if ( k > n ): return 0
  else:
    if ( n == 0 ) and ( k == 0 ): return 1
    elif n == k: return 1
    elif k == 0: return 0
    else:        return tr2[n-k][k]
 
def coef( k, t ):
  if not isinstance( k, int ): raise TypeError
  if not isinstance( t, int ): raise TypeError
  if ( k < 0 ) or ( t < 1 ): raise TypeError
  else:
    a = Fraction(0,1)
    for j in range( t - 1, k + 1, 1 ):
      b = ((-1)**(k-j)) * S(k,j) * s(j+1,t)
      a += Fraction(b,j+1)
    return a
 
for k in range( 1, 9, 1 ):
  list = [ Fraction(0,1) ]
  for t in range( 1, k + 2, 1 ):
    list.append( coef( k, t ) )
  p = Poly1( list )
  print p
  for n in [ 3, 5, 7 ]:
    sum = 0
    for i in range( 1, n + 1, 1 ):
      sum += i**k
    print "n =", n, sum, p.Horner(n)

sample4.4.3.pyの実行結果

1/2X^2 + 1/2X
n = 3 6 6
n = 5 15 15
n = 7 28 28
1/3X^3 + 1/2X^2 + 1/6X
n = 3 14 14
n = 5 55 55
n = 7 140 140
1/4X^4 + 1/2X^3 + 1/4X^2
n = 3 36 36
n = 5 225 225
n = 7 784 784
1/5X^5 + 1/2X^4 + 1/3X^3 - 1/30X
n = 3 98 98
n = 5 979 979
n = 7 4676 4676
1/6X^6 + 1/2X^5 + 5/12X^4 - 1/12X^2
n = 3 276 276
n = 5 4425 4425
n = 7 29008 29008
1/7X^7 + 1/2X^6 + 1/2X^5 - 1/6X^3 + 1/42X
n = 3 794 794
n = 5 20515 20515
n = 7 184820 184820
1/8X^8 + 1/2X^7 + 7/12X^6 - 7/24X^4 + 1/12X^2
n = 3 2316 2316
n = 5 96825 96825
n = 7 1200304 1200304
1/9X^9 + 1/2X^8 + 2/3X^7 - 7/15X^5 + 2/9X^3 - 1/30X
n = 3 6818 6818
n = 5 462979 462979
n = 7 7907396 7907396

sample4.4.3.rb

require 'mathn'
require './poly1'
 
# calculate tables
$tr1 = Array.new(10) { Array.new(10) { 0 } }
$tr2 = Array.new(10) { Array.new(10) { 0 } }
for j in 0...10
  $tr1[0][j] = 1; $tr2[0][j] = 1
end
for i in 1...10
  for j in 1...10
    $tr1[i][j] = $tr1[i][j-1] + (i+j-1) * $tr1[i-1][j]
    $tr2[i][j] = $tr2[i][j-1] +       j * $tr2[i-1][j]
  end
end
 
def s(n, k)
  if ( ! n.kind_of?(Integer) ) or ( ! k.kind_of?(Integer) )
    raise TypeError
  end
  if ( k < 0 ) or ( n < 0 ) or ( k > 9 ) or ( n > 9 )
    raise TypeError
  end
  if ( k > n )
    return 0
  else
    if ( n == 0 ) and ( k == 0 )
      return 1
    elsif n == k
      return 1
    elsif k == 0
      return 0
    else
      return $tr1[n-k][k]
    end
  end
end
 
def S(n, k)
  if ( ! n.kind_of?(Integer) ) or ( ! k.kind_of?(Integer) )
    raise TypeError
  end
  if ( k < 0 ) or ( n < 0 ) or ( k > 9 ) or ( n > 9 )
    raise TypeError
  end
  if ( k > n )
    return 0
  else
    if ( n == 0 ) and ( k == 0 )
      return 1
    elsif n == k
      return 1
    elsif k == 0
      return 0
    else
      return $tr2[n-k][k]
    end
  end
end
 
def coef(k, t)
  if ( ! k.kind_of?(Integer) ) or ( ! t.kind_of?(Integer) )
    raise TypeError
  end
  if ( k < 0 ) or ( t < 1 )
    raise TypeError
  else
    a = 0
    for j in (t-1)..k
      b = ((-1)**(k - j)) * S(k,j) * s(j+1,t)
      a += b / (j + 1)
    end
    return a
  end
end
 
for k in 1...9
  list = [0]
  for t in 1..(k+1)
    list.push(coef(k, t))
  end
  p = Poly1(list)
  print p, "\n"
  for n in [3, 5, 7]
    sum = 0
    for i in 1..n
      sum += i**k
    end
    printf "n = %d %d %d\n", n, sum, p.Horner(n)
  end
end

sample4.4.3.rbの実行結果

1/2X^2 + 1/2X
n = 3 6 6
n = 5 15 15
n = 7 28 28
1/3X^3 + 1/2X^2 + 1/6X
n = 3 14 14
n = 5 55 55
n = 7 140 140
1/4X^4 + 1/2X^3 + 1/4X^2
n = 3 36 36
n = 5 225 225
n = 7 784 784
1/5X^5 + 1/2X^4 + 1/3X^3 - 1/30X
n = 3 98 98
n = 5 979 979
n = 7 4676 4676
1/6X^6 + 1/2X^5 + 5/12X^4 - 1/12X^2
n = 3 276 276
n = 5 4425 4425
n = 7 29008 29008
1/7X^7 + 1/2X^6 + 1/2X^5 - 1/6X^3 + 1/42X
n = 3 794 794
n = 5 20515 20515
n = 7 184820 184820
1/8X^8 + 1/2X^7 + 7/12X^6 - 7/24X^4 + 1/12X^2
n = 3 2316 2316
n = 5 96825 96825
n = 7 1200304 1200304
1/9X^9 + 1/2X^8 + 2/3X^7 - 7/15X^5 + 2/9X^3 - 1/30X
n = 3 6818 6818
n = 5 462979 462979
n = 7 7907396 7907396

参考文献

[1] グレアム, クヌース, パタシェニク, コンピュータの数学, 共立出版, 1993

数　　学

昇階乗しょうかいじょう, rising factorial

昇階乗、降階乗、第1種スターリング数、第2種スターリング数を表わすときに『コンピュータの数学』において採用された記号を使用している。

降階乗こうかいじょう, falling factorial
第1種スターリング数だい1しゅすたーりんぐすう, Stirling cycle number
第1種スターリング数の三角形だい1しゅすたーりんぐすうのさんかくけい

関孝和の『括要算法』にも昇階乗を展開することにより得られた第1種スターリング数の三角形が書かれているが、関がこれと関・ベルヌーイ数との関係を知っていたかどうかは不明である。

第2種スターリング数だい2しゅすたーりんぐすう, Stirling subset number

Published by SANENSYA Co.,Ltd.