パスカルの算術三角形論

著者:梅谷武
語句:パスカル,ナーラーヤナ,算術三角形論,細胞,母数,分割線,相反細胞,算術三角形,階乗,重和,組み合わせ,二項係数,二項定理

パスカルの算術三角形論について述べる。

作成:2006-05-24
更新:2021-03-17

前節で見たように組み合わせを数の三角形で計算するという行為は、少なくとも10世紀のハラーユダ以前のインドにおいて行われていました。ハラーユダの解釈が正しければ紀元前2世紀頃のピンガラがすでに行っていたことになりますし、10世紀以前のインドの数学文献にもメールという言葉がしばしば現われています。中国においても11世紀半ばに賈憲が著した『黄帝九章算経細草』全九巻(失伝)の中にインドのメールとまったく同じ形の数の三角形により二項係数を求める二項展開を利用した算法についての記述があることを、1261年に書かれた『詳解九章算法』の中で楊輝が引用しています。

この数の三角形がパスカルの三角形と呼ばれているのは、パスカルPascal, Blaise, 1623-1662が1654年から1658年頃までの間に書いたとされる一連の論文において算術三角形を計算原理とした数列の計算法や二項展開法を整理するとともに組み合わせ論、確率論の基礎を確立し、その後の理論の発展の土台を築き上げたことによります。パスカルの死後、これらの論文は『算術三角形論Traitè du Triangle arithmètique avec quelques autres petits traitez sur la mesme matiere par Monsieur Pascal』として1665年にパリで出版されました。この節では『算術三角形論』で展開されたパスカルの理論を現代の言葉使いと代数記号を使って再現してみましょう。

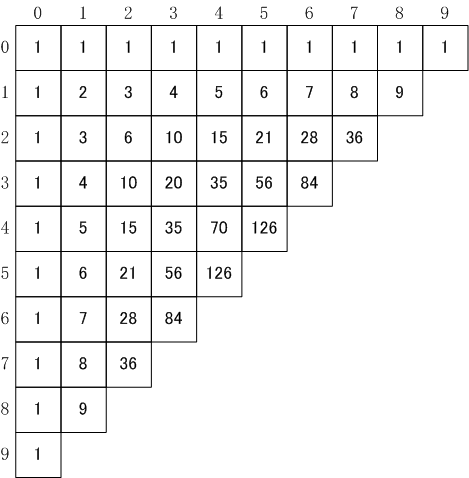
図4.2.3 パスカルの算術三角形

算術三角形はメールとは少し異なり、正方形の桝目は将棋盤のように配置され、原点を左上にとります。桝目は細胞さいぼう, cellules(fr)と呼ばれます。各細胞にはその行番号と列番号により座標が付けられます。左上隅にある細胞の座標が(0,0)です。この細胞から水平方向右側へ向かう細胞の座標は順に(0,1),(0,2),⋯となり、垂直方向下側へ向かう細胞の座標は順に(1,0),(2,0),⋯となります。各細胞の座標(i,j)におけるiを行指数、jを列指数と呼びます。各細胞に置かれる数をその座標(i,j)を使ってC(i,j)と書くことにします。C(0,0)を母数ぼすう, generateur(fr)と呼びます。算術三角形は母数を与えることにより、次の規則によって生成されます。

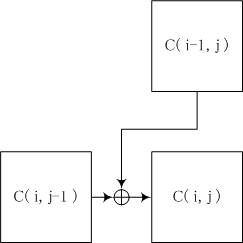
C(i,j) = C(i－1,j) + C(i,j－1), (i,j) ∈ℕ × ℕ

図4.2.5 生成規則

上の式においてC(－1,j)=C(i,－1)=0, i,j∈ℕと考えます。言い換えれば、各細胞の値は左の細胞の値と上の細胞の値の和になっています。これはインド数学のメールを左に傾けて、直角三角形にしたものと考えてかまいません。左に傾けたために三角形の底辺は水平方向に対して45度傾くことになりました。そのため現在では算術三角形を変形して底辺が水平になるようにして使うことがよくあります。

sample4.2.1.py

max = 10
C = [[0 for j in range(max)] for i in range(max)]
C[0][0] = 1
for i in range(1,max):
  C[i][0] = 1
for j in range(1,max):
  C[0][j] = 1
for i in range(1,max):
  for j in range(1,max-i):
    C[i][j] = C[i-1][j] + C[i][j-1]
 
for i in range(max):
  for j in range(max-i):
    print " %3d" % C[i][j],
  print "\n"

sample4.2.1.pyの実行結果

   1    1    1    1    1    1    1    1    1    1 
 
   1    2    3    4    5    6    7    8    9 
 
   1    3    6   10   15   21   28   36 
 
   1    4   10   20   35   56   84 
 
   1    5   15   35   70  126 
 
   1    6   21   56  126 
 
   1    7   28   84 
 
   1    8   36 
 
   1    9 
 
   1

sample4.2.1.rb

max = 10
C = Array.new(max) { Array.new(max) { 0 } }
C[0][0] = 1
for i in 1...max
  C[i][0] = 1
end
for j in 1...max
  C[0][j] = 1
end
for i in 1...max
  for j in 1...(max-i)
    C[i][j] = C[i-1][j] + C[i][j-1]
  end
end
 
for i in 0...max
  for j in 0...(max-i)
    printf " %3d", C[i][j]
  end
  print "\n\n"
end

sample4.2.1.rbの実行結果

   1   1   1   1   1   1   1   1   1   1
 
   1   2   3   4   5   6   7   8   9
 
   1   3   6  10  15  21  28  36
 
   1   4  10  20  35  56  84
 
   1   5  15  35  70 126
 
   1   6  21  56 126
 
   1   7  28  84
 
   1   8  36
 
   1   9
 
   1

座標(i,j)の細胞が属する底辺の指数をi+jで定義します。これは底辺の数列が頂点から何番目にあるかということを示しています。例えば指数が2の底辺の数列は1,2,1、指数が3の底辺の数列は1,3,3,1となっています。

図4.2.12 底辺と分割線

算術三角形の底辺から垂直に原点へ向かう法線を分割線ぶんかつせん, dividente(fr)といいます。算術三角形は図形としてこの分割線に関して対称になっていますから、この細胞をこの分割線を中心にして180度回転すると別の細胞に重なります。この細胞のことを相反細胞そうはんさいぼう, reciproques(fr)といいます。ある細胞の座標を(i,j)とするとその相反細胞の座標は(j,i)となります。

算術三角形さんじゅつさんかくけい, triangle arithmètique(fr)とは原点(0,0)を頂点とし、ある指数の底辺までの細胞全体が成す三角形のことです。パスカルはこの算術三角形に関する性質を次に示す19の帰結としてまとめています。

命題4.2.15 算術三角形に関する19の帰結

任意の母数の算術三角形について以下に示す帰結が導き出される。特に指定がない場合、i,j,kは任意の自然数と考える。

(P1)

第0行と第0列のすべての細胞は母細胞と同じである。

C(0,0) = C(0,j) = C(i,0)

(P2)

各細胞はその上の行の左端からその細胞の上までのすべての細胞の和に等しい。

C(i,j) =

j
∑
k=0

C(i－1,k)

(P3)

各細胞はその左の列の上端からその細胞の左までのすべての細胞の和に等しい。

C(i,j) =

i
∑
k=0

C(k,j－1)

(P4)

各細胞から1を引いたものはその細胞を含む行の上側と列の左側との間のその行と列は除いた部分に含まれるすべての細胞の和に等しい。

C(i,j) － 1 =

j－1
∑
t=0

i－1
∑
s=0

C(s,t)

(P5)

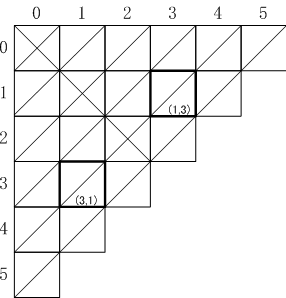
各細胞はその相反細胞に等しい。

C(i,j) = C(j,i)

(P6)

行指数と列指数が同じ値kをもつ第k行と第k列はまったく同じ細胞から成っている。

(C(k,j))_{j ∈ℕ} = (C(i,k))_{i ∈ℕ}

(P7)

各底辺の細胞の和は、その上の底辺の細胞の和の2倍である。

∑
i+j=k

C(i,j)

= 2

∑
i+j=k－1

C(i,j)

(P8)

各底辺の細胞の和は、1から始まる公比2の等比級数の一項であり、その指数は底辺の指数と同じである。

∑
i+j=k

C(i,j)

= 2^k

(P9)

各底辺の細胞の和から1を引いたものは、それより上のすべての底辺の細胞の和に等しい。

∑
i+j=k

C(i,j)

－ 1 =

k－1
∑
r=0

(

∑
i+j=r

C(i,j)

)

k－1
∑
r=0

2^r

(P10)

ある底辺の一端から連続した細胞列の和は、その上の底辺の一端から同じ長さの細胞列の和に、長さを一つ減じた細胞列の和を加えたものに等しい。

n
∑
j=0

C(k－j,j)

n
∑
j=0

C(k－1－j,j)

n－1
∑
j=0

C(k－1－j,j)

(P11)

分割線上の細胞はその上または左で隣り合う細胞の2倍である。

C(i,i) = 2C(i,i－1) = 2C(i－1,i)

(P12)

同じ底辺にあって隣接する二つの細胞について上の細胞と下の細胞との比は、上の細胞から底辺の最上段までの細胞の個数と下の細胞から底辺の最下段までの細胞の個数との比に等しい。

C(i,j) : C(i+1,j－1) = i + 1 : j

(P13)

同じ列にあって隣接する二つの細胞について下の細胞と上の細胞との比は、上の細胞の底辺の指数に1を加えたものと行指数に1を加えたものとの比に等しい。

C(i+1,j) : C(i,j) = i + j + 1 : i + 1

(P14)

同じ行にあって隣接する二つの細胞について右の細胞と左の細胞との比は、左の細胞の底辺の指数に1を加えたものと列指数に1を加えたものとの比に等しい。

C(i,j+1) : C(i,j) = i + j + 1 : j + 1

(P15)

ある行の細胞の和と同じ行の右端の細胞との比は、底辺の指数に1を加えたものとその行指数に1を加えたものとの比に等しい。

j
∑
k=0

C(i,k)

: C(i,j) = i + j + 1 : i + 1

(P16)

ある行の細胞の和とその下の行の細胞の和との比は、下の行の指数に1を加えたものとその行の細胞の個数との比に等しい。

j
∑
k=0

C(i,k)

j－1
∑
k=0

C(i+1,k)

= i + 2 : j

(P17)

ある細胞にそれを含む列の上側のすべての細胞を加えたものと同じ細胞にそれを含む行の左側のすべての細胞を加えたものとの比は、それぞれの細胞の個数の比に等しい。

i
∑
k=0

C(k,j)

j
∑
k=0

C(i,k)

= i + 1 : j + 1

(P18)

上下端から等距離にある二つの行の細胞の和の比は、それらの細胞の個数の比に等しい。

k－i
∑
j=0

C(i,j)

i
∑
j=0

C(k－i,j)

= k － i + 1 : i + 1

(P19)

分割線上にあって隣接する二つの細胞について、下の細胞と上の細胞の4倍との比は、上の細胞の底辺の指数に1を加えたものとさらにそれに1を加えた数との比に等しい。

C(i,i) : 4C(i－1,i－1) = 2i － 1 : 2i

証明

演習とする。■

パスカルは12番目の帰結の証明において数学的帰納法の原理を明確に述べています。このことからパスカルが数学的帰納法の創始者であるとされています。

算術三角形においては母数は任意の数をとりうるのですが、その作り方からわかるように母数nが1と異なる場合の算術三角形は、母数が1の場合の算術三角形の全体にnを掛けたものと等しくなっています。またパスカル自身も算術三角形の応用に際しては母数が1の場合に限っています。以後、算術三角形の母数は1であると仮定することにします。

任意の自然数i,jを与えたときにC(i,j)を算術三角形を使わないで計算する方法についてパスカルは次の命題を示しています。

命題4.2.20 算術三角形の階乗公式

任意の自然数i,j(j>0)に対して次の式が成り立つ。

(4.1)

C(i,j) =

(i+1)⋯(i+j)

証明

C(i,j)とその底辺の左端の細胞1との比は(P12)より、

C(i,j)

C(i+1,j－1)

C(i+2,j－2)

⋯

C(i+j－1,1)

C(i+j,0)

i+1

i+2

j－1

⋯

i+j

■

上の式で正の整数kについてkの狭義の階乗かいじょう, factorialk!を

k! = 1 ⋅ 2 ⋅ 3 ⋅ ⋯ ⋅ k

によって定義しています。0の階乗については便宜上0!=1と定義します。広い意味では(i+1)⋯(i+j)も階乗と考えますが、これについては後で詳しく述べることにします。

上の公式で実際に計算するときは(P5)を使って積の長さが短くなるようにします。

例題4.2.24

C(2,4)を計算せよ。

解答

C(2,4) = C(4,2) =

5 ⋅ 6

2 ⋅ 1

= 15

■

重和

ナーラーヤナNarayana, 14世紀のインドの数学者。は1356年に著した『ガニタカウムディー』において重和じゅうわ, vārasa\d{m}kalitaという概念を導入しました。算術三角形を使うとこれをうまく表現することができます。算術三角形の第0行は1,1,1,⋯というように単位数が続く数列になっています。この数列の初項からn番目の項までの和を0次の重和といいます。

(4.2)

S₀(n) = 1 + 1 + 1 + ⋯ + 1 (n個の和)

0次の重和数列(S₀(n))_n∈ℕは単位数から始まる自然数列1,2,3,⋯ですが、(P2)によってS₀(n) = C(1,n－1)が成り立ちますから、これは算術三角形の第1行そのものです。この重和をとったものが1次の重和です。

S₁(n) =

n
∑
i=1

S₀(i)

= C(2,n－1) = 1 + 2 + 3 + ⋯ + n

これは三角数Δ_nに他なりません。2次の重和

S₂(n) =

n
∑
i=1

S₁(i)

= C(3,n－1) = 1 + 3 + 6 + ⋯ +

n(n+1)

は四面体数Tet_nになっています。3次の重和

S₃(n) =

n
∑
i=1

S₂(i)

= C(4,n－1) = 1 + 4 + 10 + ⋯ +

n(n+1)(n+2)

は五胞体数と呼ばれています。一般に正の整数kに対してk次の重和は

(4.3)

S_k(n) =

n
∑
i=1

S_k－1(i)

, k > 0

によって定義されます。上で見たように算術三角形の第k行はk－1次の重和数列になっています。(P2)によってS_k(n) = C(k+1,n－1) = C(n－1,k+1)が成り立ちますから、階乗公式によって次の式を得ることができます。

命題4.2.27 算術三角形と重和

任意の自然数n,kに対して次の式が成り立つ。

(4.4)

S_k(n) =

n(n+1)⋯(n+k)

(k+1)!

, k ≧ 0

組み合わせ

紀元前6世紀のインドの医学書「スシュルタ」に、苦・酸・塩・渋・甘・辛の6種類の味覚から63種類の組み合わせが作られるということが書かれていますが、これが組み合わせに関する最古の数学的な記述であると考えられています。一般にn個のものから順序を考えず重複を許さないでちょうどk個だけ取り出す組み合わせくみあわせ, combinationの数を

(

n
k

)

と書きます。便宜上、任意の自然数nについて

(

n
0

)

と考えます。

上の問題を実際に解いてみましょう。6種類の味覚の一つだけ使うときの選び方は、

{ 苦,酸,塩,渋,甘,辛 }

という6通り、

(

6
1

)

= 1+1+1+1+1+1 = 6

です。二つ使うときの選び方は、

{

苦酸,苦塩,苦渋,苦甘,苦辛,

酸塩,酸渋,酸甘,酸辛,

塩渋,塩甘,塩辛,

渋甘,渋辛,

甘辛 }

という15通り、

(

6
2

)

= 1+2+3+4+5 = 15

です。三つ使うときの選び方は

{

苦酸塩,苦酸渋,苦酸甘,苦酸辛,

苦塩渋,苦塩甘,苦塩辛,

苦渋甘,苦渋辛,

苦甘辛,

酸塩渋,酸塩甘,酸塩辛,

酸渋甘,酸渋辛,

酸甘辛,

塩渋甘,塩渋辛,

塩甘辛,

渋甘辛 }

という20通り、

(

6
3

)

= (1)+(1+2)+(1+2+3)+(1+2+3+4) = 20

です。四つ使うときの選び方は、二つ使わないと考えれば

(

6
4

)

(

6
2

)

= 15

です。五つ使うときの選び方は一つ使わないと考えれば

(

6
5

)

(

6
1

)

= 6

です。六つ使うときの選び方は

(

6
6

)

= 1

です。これらの合計をとると

6
∑
k=1

(

6
k

)

= 6 + 15 + 20 + 15 + 6 + 1 = 63

となります。

上で解いていく過程を観察すると、

(

6
1

)

S₀(6) = C(1,5)

(

6
2

)

S₁(5) = C(2,4)

(

6
3

)

S₂(4) = C(3,3)

(

6
4

)

(

6
2

)

(

6
5

)

(

6
1

)

が成り立っていることがわかります。しかも、この場合だけではなく一般にも成り立ちそうですが、これをどうやって証明したらいいのでしょうか。パスカルはこれが一般に成り立つことを組み合わせの考え方を使って証明しました。まず、次の補題を準備しています。

補題4.2.31 組み合わせの加法公式

任意の自然数a,b(a＜b)に対して次の式が成り立つ。

(4.5)

(

b
a

)

(

b
a+1

)

(

b+1
a+1

)

証明

a=0のときは

1 +

(

b
1

)

(

b+1
1

)

となり、自明である。a>0とする。

(

b+1
a+1

)

をb+1個の文字からa+1個取り出す組み合わせと考える。b+1個の文字にある特定の文字`c'が含まれているものとする。a+1個取り出す組み合わせには文字`c'を含むものと含まないものがある。文字`c'を含むものの数は

(

b
a+1

)

に等しい。文字`c'を含むものについてはその組み合わせから文字`c'を取り去ることによって、その個数が

(

b
a

)

であることがわかる。■

そしてこの補題を使って、底辺の指数に関する数学的帰納法で次の定理を証明しています。

命題4.2.34 算術三角形と組み合わせ

任意の自然数i,jに対して次の式が成り立つ。

(4.6)

C(i,j)=

(

i+j
j

)

証明

C(0,0)=C(0,1)=C(1,0)=1より、指数1の算術三角形においては成り立つ。i,jをi+j=k＞0なる自然数とし、指数kの算術三角形において式が成り立つと仮定する。指数k+1の算術三角形の底辺上の細胞C(i,j+1),C(i+1,j)について、算術三角形の定義と補題から次が成り立つ。

C(i,j+1)

C(i,j)+C(i－1,j+1)

(

i+j
j

)

(

i+j
j+1

)

(

i+j+1
j+1

)

C(i+1,j)

C(i+1,j－1) + C(i,j)

(

i+j
j－1

)

(

i+j
j

)

(

i+j+1
j

)

したがって指数k+1の算術三角形の任意の細胞において式が成り立つ。■

この関係式により、現代においては二項係数の定義として使われている次の等式を証明することができます。

系4.2.37

任意の自然数n,k(n ≧ k)に対して次の式が成り立つ。

(4.7)

(

n
k

)

(n－k)!k!

証明

k>0のときは、

(

n
k

)

=C(n－k,k)=

n(n－1)⋯(n－k+1)

(n－k)!k!

より、k=0のときは0!=1と

(

n
0

)

= 1

より、いずれの場合も等式が成り立つ。■

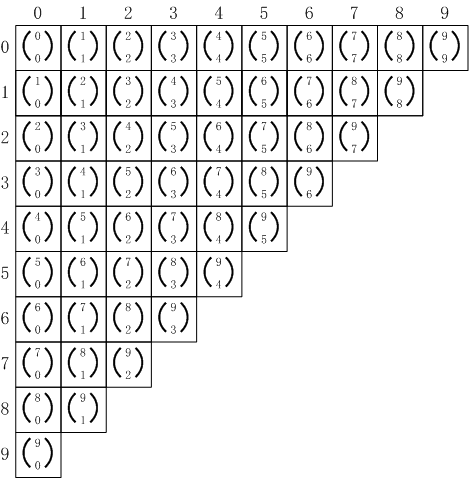
実際にはC(i,j)よりも

(

n
k

)

を使うことが多いので、算術三角形に関する19の帰結を組み合わせの言葉で書き直しておくことにします。

命題4.2.40 組み合わせに関する19の帰結

特に指定がない場合、n,k(n ≧ k)は任意の自然数と考える。

(P'1)

(

0
0

)

(

n
n

)

(

n
0

)

= 1

(P'2)

(

n
k

)

k
∑
i=0

(

n－k－1+i
i

)

(P'3)

(

n
k

)

n－k
∑
i=0

(

k+i
k

)

(P'4)

(

n
k

)

－ 1 =

n－k－1
∑
i=0

k－1
∑
j=0

(

i+j
j

)

(P'5)

(

n
k

)

(

n
n－k

)

(P'6)

(

k+j
j

)

)_{j ∈ℕ} = (

(

i+k
k

)

)_{i ∈ℕ}

(P'7)

n
∑
i=0

(

n
i

)

= 2

n－1
∑
i=0

(

n－1
i

)

(P'8)

n
∑
i=0

(

n
i

)

= 2ⁿ

(P'9)

n
∑
i=0

(

n
i

)

－ 1 =

n－1
∑
r=0

(

r
∑
i=0

(

r
i

)

) =

n－1
∑
r=0

2^r

(P'10)

r
∑
i=0

(

n
i

)

r
∑
i=0

(

n－1
i

)

r－1
∑
i=0

(

n－1
i

)

(P'11)

(

2n
n

)

= 2

(

2n－1
n－1

)

= 2

(

2n－1
n

)

(P'12)

(

n
k

)

n－k+1

(

n
k－1

)

(P'13)

(

n
k

)

n－k

(

n－1
k

)

(P'14)

(

n
k

)

(

n－1
k－1

)

(P'15)

k
∑
i=0

(

n－k+i
i

)

n+1

n－k+1

(

n
k

)

(P'16)

k
∑
i=0

(

n－k+i
i

)

n－k+2

k－1

k－1
∑
i=0

(

n－k+1+i
i

)

(P'17)

n－k
∑
i=0

(

k+i
i

)

n－k+1

k+1

k
∑
i=0

(

n－k+i
i

)

(P'18)

k
∑
i=0

(

n－k+i
i

)

k+1

n－k+1

n－k
∑
i=0

(

k+i
i

)

(P'19)

(

2n
n

)

2n－1

(

2n－2
n－1

)

証明

演習とする。■

算術三角形を組み合わせを使って書いておきます。

図4.2.43 組み合わせで表現した算術三角形

二項定理

n個のものからk個とる組み合わせ

(

n
k

)

は二項係数にこうけいすう, binomial coefficientと呼ばれています。これは次に示す二項定理にこうていり, binomial theoremに由来しています。

可換環R上の二変数多項式X+Y ∈R[X,Y]を自然数nで冪乗することについて考えます。

(X+Y)ⁿ = (X+Y)(X+Y)⋯(X+Y) (n個の積)

これを展開するとn次の単項式の和、すなわちn次の斉次式になります。各単項式はn個のX+YからXかYのどちらかを選び出したものです。可換性からこれは

X^kY^n－k, k = 0, ⋯, n

と書くことができますが、この単項式の個数はn個のX+Yからk個のXをとる組み合わせ

(

n
k

)

に他なりません。したがって次の定理が成り立ちます。

定理4.2.46 二項定理

可換環上の二変数多項式と任意の自然数nについて次が成り立つ。

(4.8)

(X+Y)ⁿ =

n
∑
k=0

(

n
k

)

X^kY^n－k

多項定理

(原稿未完成)

参考文献

[1] 林隆夫, インドにおける順列・組み合わせ・列挙, 科学史研究[第2期], vol.18, 158-171, 1979

[2] 楠葉隆徳, 矢野道雄, 林隆夫, インド数学研究, 恒星社厚生閣, 2003

[3] 伊東俊太郎, 数学の歴史(2) 中世の数学, 共立出版, 1987

[4] ヴィクター・J. カッツ, カッツ数学の歴史, 共立出版, 2005

[5] 伊吹武彦, パスカル全集〈第1-3巻〉, 人文書院, 1967

人　　物

パスカル Pascal, Blaise, 1623-1662

フランスの数学者・物理学者。

ナーラーヤナ Narayana, 14世紀のインドの数学者。

物　　品

算術三角形論 Traitè du Triangle arithmètique avec quelques autres petits traitez sur la mesme matiere par Monsieur Pascal

一部の日本語訳が伊吹武彦他訳, 『パスカル全集』, 第1巻, 人文書院, 1978(原亨吉訳, 数学論文集) に含まれている。

数　　学

細胞さいぼう, cellules(fr)
母数ぼすう, generateur(fr)
分割線ぶんかつせん, dividente(fr)
相反細胞そうはんさいぼう, reciproques(fr)
算術三角形さんじゅつさんかくけい, triangle arithmètique(fr)
階乗かいじょう, factorial
重和じゅうわ, vārasa\d{m}kalita
組み合わせくみあわせ, combination
二項係数にこうけいすう, binomial coefficient
二項定理にこうていり, binomial theorem

Published by SANENSYA Co.,Ltd.