紀元前2600年頃から紀元前1800年頃までの間、現在のインドとパキスタンにまたがるインダス川周辺に都市文明が栄えていました。ドラヴィダ語族のドラヴィダ人によるものとされるこのインダス文明は、その後、地殻変動などにより主要な都市が放棄され、衰退します。紀元前15世紀頃からこの地域にインド・ヨーロッパ語族のアーリア人が侵入します。アーリア人はカースト制と呼ばれる階級制度により先住民であるドラヴィダ系民族を支配しました。その階級の頂点に立ったのがバラモン教の司祭であるブラフマンです。紀元前1200年頃からブラフマン達は口伝により伝えられてきたヴェーダと呼ばれる宗教上の知識を文書として編簒し始めます。紀元前600年頃になるとさらにそのヴェーダの手引書が編簒され始めます。これらの多くには糸という意味の「スートラ」という名が付けられましたが、これは伝統的に「経」と漢訳されています。これらの手引書はヴェーダーンガ(ヴェーダ補助学)として体系化され、その内容は音声学・韻律学・文法学・語源学・祭儀学・暦法学の6種類に分類されています。

 紀元前200年頃、ピンガラは『チャンダハスートラ』を著し、これによりヴェーダの韻律学が確立しました。『チャンダハスートラ』は記憶するための簡潔なスートラ体で著されているために解読が困難で、10世紀後半にハラーユダによって著された注釈書『ムリタサンジーヴァニー』によって間接的にピンガラの韻律学を解釈することができます。『チャンダハスートラ』は組み合わせの問題を数学的に扱った現存する最古の文献ではないかと考えられています。またハラーユダの解釈によれば、組み合わせの数を求めるために、後にインド数学においてメールと呼ばれるようになる算術三角形を使っています。この節では、文献[1],[2]を参考にしてピンガラの韻律学を再現してみましょう。

 ヴェーダの一つの詩節の四分の一を1パーダといいます。この各パーダを構成する音節数と各音節の軽(laghu)・重(guru)によって韻律が定まります。これをヴリッタといいます。ヴェーダの韻律学では1パーダの音節数nが与えられたときに、すべての可能なヴリッタを列挙すること(展開図表)、展開図表の番号から対応するヴリッタを知ること(消失)、逆に ヴリッタからその展開図表における番号を知ること(提示)、軽音節数kが与えられたときにk個の軽音節をもつヴリッタの個数を求めること(軽音節計算)、すべての可能なヴリッタの総数を求めること(数)、という五つが問題になります。

 現代から見るとこれは、0と1という二つの状態を持つ情報の単位をbitと呼ぶことにしたとき、n bitで表現可能なすべての2進符号を列挙すること(展開図表)、展開図表の番号から対応するn bit符号を知ること(消失)、逆にn bit符号からその展開図表における番号を知ること(提示)、数kが与えられたときにk個の0をもつn bit符号の個数を求めること(軽音節計算)、すべての可能なn bit符号の総数を求めること(数)、という問題に対応していることに気が付きます。消失と提示はそれぞれ符号化と復号に相当します。

展開図表

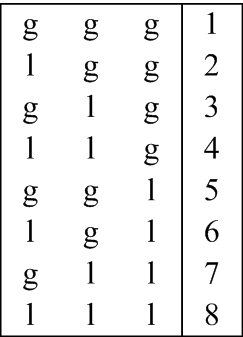
 軽音節をl、重音節をgで表します。例として3音節の場合を考えると展開図表は次の手順で作られます。(1) 左側の列に2組のgとlを置く、(2) その右側の列に2つ連続したgとlを置く、(3) これを2組縦に並べ、(4) その右側に4つ連続したgとlを置く。

 これは言い換えればg＜lとして右から見て辞書式順序になるように並べていることになります。3音節の場合の展開図表を図に示します。この展開図表が3音節から成るすべての可能なヴリッタを示しています。

消失

 展開図表で上から順に番号を付けます。この番号を与えたときに対応するヴリッタのgとlの配列を知る方法が「消失」です。音節数nと展開図表の番号mが与えられたときに対応 するヴリッタを求めるピンガラの消失算法をPythonで記述してみます。

sample4.1.1.py

def encode( n, m ):
  str = []
  for i in range( n ):
    if m % 2 == 0:
      m = m / 2
      str.append( 'l' )
    else:
      m = ( m + 1 ) / 2
      str.append( 'g' )
  return ''.join( str )
 
for i in range( 1, 9, 1 ):
  print '%s %d' % ( encode( 3, i ), i )

sample4.1.1.pyの実行結果

ggg 1
lgg 2
glg 3
llg 4
ggl 5
lgl 6
gll 7
lll 8

sample4.1.1.rb

def encode(n, m)
  str = []
  for i in 0...n
    if m % 2 == 0
      m = m / 2
      str.push('l')
    else
      m = (m + 1) / 2
      str.push('g')
    end
  end
  return str.join
end
 
for i in 1...9
  printf "%s %d\n", encode(3, i), i
end

sample4.1.1.rbの実行結果

ggg 1
lgg 2
glg 3
llg 4
ggl 5
lgl 6
gll 7
lll 8

提示

 提示は消失の逆です。ヴリッタが与えられたときにその展開図表の番号を求めます。音節数nとヴリッタが与えられたときに対応する展開図表の番号を求めるピンガラの提示算法をPythonで記述してみます。

sample4.1.2.py

def decode( n, vrtta ):
  if isinstance( vrtta, str ):
    if len( vrtta ) != n:
      raise TypeError
    else:
      a = 1
      for i in range( n ):
        if vrtta[n-1-i] == 'l':
          a = 2 * a
        elif vrtta[n-1-i] == 'g':
          a = 2 * a - 1
        else:
          raise TypeError
      return a
  else:
    raise TypeError
 
table = ["ggg","lgg","glg","llg","ggl","lgl","gll","lll"]
for vrtta in table:
  print '%s %d' % ( vrtta, decode( 3, vrtta ) )

sample4.1.2.pyの実行結果

ggg 1
lgg 2
glg 3
llg 4
ggl 5
lgl 6
gll 7
lll 8

sample4.1.2.rb

def decode(n, vrtta)
  if vrtta.kind_of?(String)
    if vrtta.length != n
      raise TypeError
    else
      a = 1
      for i in 0...n
        if vrtta[n-1-i].chr == 'l'
          a = 2 * a
        elsif vrtta[n-1-i].chr == 'g'
          a = 2 * a - 1
        else
          raise TypeError
        end
      end
      return a
    end
  else
    raise TypeError
  end
end
 
table = ["ggg","lgg","glg","llg","ggl","lgl","gll","lll"]
for vrtta in table
  printf "%s %d\n", vrtta, decode(3, vrtta)
end

sample4.1.2.rbの実行結果

ggg 1
lgg 2
glg 3
llg 4
ggl 5
lgl 6
gll 7
lll 8

軽音節計算

 音節数nとその軽音節数kが与えられたときに可能なヴリッタの数を求めることを軽音節計算といいます。これはn個のものからk個を取り出す組み合わせの数 に他なりません。組み合わせについては次節で詳細に調べることになりますので、ここでは触れません。

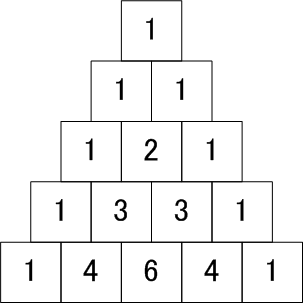
 ハラーユダは、ピンガラはメール^*1と呼ばれる数の三角形を使ってこれを計算したと解釈しています。メールの作図法ですが、まず山の頂上の部分に正方形の枡目を書き、その下に両側に半分だけはみ出るように二つの桝目を書く、さらにその下には三つ、さらにその下には四つというように必要なだけ桝目を書いていきます。そして頂上の桝目には1を入れ、その下の桝目は両端には1を入れ、間の桝目にはその上にある桝目の数の和を入れるという規則で数を埋めていきます。このようにして完成したメールのn+1行目の左からk+1番目の桝目に入っている数が となっています。

数

 音節数nを与えたときに可能なヴリッタの総数を求めることが「数」と呼ばれています。このヴリッタの総数2ⁿを求めるピンガラの算法は第1章1.5節で紹介した繰り返し二乗法と同じものです。

参考文献