一意分解整域
著者:梅谷 武
語句:一意分解整域,アイゼンシュタイン,商体,原始的,原始多項式,容量,ガウスの補題
一意分解整域上の多項式環が一意分解整域になることについて述べる。
作成:2006-05-19
更新:2021-03-17
2変数以上の体上の多項式環は一変数の場合とは異なり、単項イデアル整域にはなりません。例えば、体上の2変数多項式環k[X,Y]において(X,Y)は単項イデアルにはなりません。このことからユークリッド整域にもなり得ないことがわかります。しかし、やはり一意分解整域となり、0でも単元でもない元は素元の積として一意的に分解することができます。また、一変数多項式環であっても係数環が体でなければ、やはり単項イデアル整域にはなりません。例えば、整数ℤ上の多項式環ℤ[X]において、単元±1以外のa ∈ℤについて(a,X)は単項イデアルにはなりません。この節の目的は一意分解整域上の多項式環が一意分解整域となること、そしてその結果として体上の多変数多項式環が一意分解整域となることを示すことです。
まず、整数から有理数を構成した同じやり方で、一般の整域
Rに対して、それを含む最小の体
Kを構成します。
Rの元を分母と分子とする分数全体の集合
Frac(R)を考えます。
| Frac(R) ≔ | 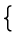 | | 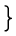 |
|
この集合において
ab'=a'bのとき
とする同値関係
∽を考え、
K = Frac(R)/∽と定義します。また
a∈Rを
と同じとみなすことによって
R⊂Kと考えます。
K上に加法と乗法を次のように定義します。
Kはこの加法と乗法によって体となります。これを
Rの
商体しょうたい, quotient fieldといいます。
Rが一意分解整域のときは、その商体
Kの元の分母と分子を素元分解し、共通因子を消去することによって、それ以上約分できないような既約表示にすることができます。また、任意の2元について最大公約元、最小公倍元が単元倍を除いて定まります。
R上の多項式
f(X) = a0 + a1 X + a2 X2 + ⋯ + an Xnにおいて、係数の最大公約元
gcd(a0, a1, ⋯, an)が
1である多項式を
原始的げんしてき, primitiveである、もしくは
原始多項式げんしたこうしき, primitive polynomialといいます。
Rの商体を
Kとし、
K上の多項式
f(X)を考えます。
f(X)の各係数を既約表示にし、分母の最小公倍元
bを乗ずると係数はすべて
Rの元となりますが、これらの最大公約元を
aとすると
c(f)=a/bとして、
| f(X) = c(f) f0(X), c(f)∈K, f0(X)∈R[X]:原始多項式
|
と分解することができます。この分解は単元倍を除いて一意的に定まります。この
c(f)を
fの
容量ようりょう, contentといいます。
一意分解整域上の多項式環において、原始多項式の積は原始多項式である。
証明
| | | = a0 + a1X + a2X2 + ⋯ + anXn |
|
| | | = b0 + b1X + b2X2 + ⋯ + bmXm |
|
を原始多項式とし、その積
について考える。もしこれが原始多項式でないとすれば、素元
pが存在して、
p|ck, k=0,⋯,m+nとなる。
f(X),g(X)は原始的であるから、そのすべての係数が
pで割れることはない。
そこで
ar,bsを
pで割れない最小次数の係数とする。
f(X)g(X)の
Xr+sの係数
| cr+s = (a0br+s + ⋯ + ar-1bs+1) + arbs + ( ar+1bs-1 + ⋯ + ar+sb0)
|
において
p∤arbsであるが、その他の項はすべて
pで割り切れる。これは
p∤cr+sであることを意味し、仮定に矛盾する。■
Rを一意分解整域、
Kをその商体とする。
K[X]の任意の多項式
f,gについて次が成り立つ。
証明
fg=c(f)c(g)f0g0においてf0g0は原始的である。■
Rを一意分解整域、
Kをその商体とする。
R[X]の既約多項式は
K[X]においても既約である。
証明
f ∈R[X]を既約多項式とするとfは原始的であり、c(f) = 1である。f=ghをK[X]における分解とすると、f=c(f)f0 = c(g)c(h)g0h0においてc(g)c(h) = c(f) = 1であるからg,hのどちらかが単元となり、fはK[X]においても既約である。■
さて、次に一意分解整域上の多項式環が一意分解整域であることを証明しますが、その前に一意分解整域上の多項式環における素元がどのようなものかを調べておきましょう。
Rを一意分解整域とし、Kをその商体とします。f,g∈R[X]についてfg=1が成り立てば、次数を考えることでf,g ∈Rであることがわかります。したがってRとR[X]の単元の集合は一致します。同じように次数を考えることでRの0でも単元でもない元がRの素元であることとR[X]の素元であることは同じことです。次数が1以上の多項式q∈R[X]を考えましょう。もしqが素元であれば、その分解c(q)q0においてc(q)=1でなければなりません。すなわち、qは既約な原始多項式でなければなりません。逆にqを既約な原始多項式であるとします。f,g∈R[X]についてR[X]においてq|fgであるならば、qはK[X]の素元ですから、K[X]においてq|fまたはq|gが成り立っていますが、ガウスの補題によりこれはR[X]においても成り立っています。したがってqはR[X]の素元です。これらのことを命題としてまとめておきましょう。
一意分解整域
R上の多項式環
R[X]において次が成り立つ。
| (1)
| RとR[X]の単元は一致する。
|
| (2)
| R[X]の素元はRの素元か既約な原始多項式である。
|
証明
Rを一意分解整域、
Kをその商体とする。
0でも単元でもない多項式
f ∈R[X]を容量
c(f)と原始多項式
f0の積
f = c(f)f0に分解する。
c(f)は
Rの元であるから、
c(f)=p1 ⋯ prと
Rにおいて素元分解することができ、それはまた
R[X]における素元分解にもなっている。
f0はまず
K[X]において既約多項式の積に分解して、
f0 = q1 ⋯ qsとなるが、各
qiにその各係数の最小公倍元
aiをかけて
ai qi ∈R[X]となるようにし、それを容量
bi = c(ai qi) ∈Rと原始多項式
qi'の積に分解することができるので、
a1 ⋯ as f0 = b1 ⋯ bs q1' ⋯ qs'と書くことができる。
c = a1 ⋯ as b1-1 ⋯ bs-1とおくと
cf0=q1' ⋯ qn'となるが、ガウスの補題により
cは
Rの単元であり、
qi'のいずれかに
c-1をかけることによって
を
R[X]における素元分解とすることができる。整域における素元分解は一意的であったから
R[X]は一意分解整域である。■
R上の多変数多項式環はR[X1,⋯,Xn] = (R[X1,⋯,Xn-1])[Xn]というように帰納的に定義されましたから、この定理から任意変数の多項式環が一意分解整域であることがわかります。
一意分解整域上の多変数多項式環は一意分解整域である。特に体上の多変数多項式環は一意分解整域である。
一意分解整域
R上の次数が
1以上の多項式
f(X)= a0 + a1 X + a2 X2 + ⋯ + an Xnについて、もし
Rの素元
pで次の条件を満たすものが存在すれば、
f(X)は
R[X]において既約である。
| (1)
| p ∤ an |
| (2)
| p | ai, i = 0, ⋯, n-1 |
| (3)
| p2 ∤ a0 |
証明
fが可約であると仮定すれば、
f=gh, deg g ≧ 1, deg h ≧ 1となる多項式
| | | b0 + b1X + b2X2 + ⋯ + blXl |
|
| | | c0 + c1X + c2X2 + ⋯ + cmXm |
|
が存在する。
b0 c0 = a0で
p | a0, p2 ∤ a0であるから、
pは
b0と
c0のどちらか一方のみを割る。
p | b0, p ∤ c0としても一般性は失わない。
p ∤ anより、
pは
biのすべてを割ることはない。
rを
p ∤ brとなる最小の添え字とする。このとき
| p | b0, ⋯, p | br-1, p ∤ br, 0 < r < n
|
となっている。
f(X)=g(X)h(X)の
Xrの係数
arを考える。
| ar = b0 cr + ⋯ + br-1 c1 + br c0
|
であるが、それ以外の項は
pで割れるので
p | arとなるがこれは仮定に矛盾する。■
[
2] ファン・デル・ヴェルデン, 現代代数学〈1〉, 商工出版社, 1959
[
4] 堀田 良之, 岩波講座 現代数学の基礎〈9〉環と体, 岩波書店, 2001
人 物
アイゼンシュタイン Eisenstein, Ferdinand Gotthold Max, 1823-1852
数 学
商体 しょうたい, quotient field
原始的 げんしてき, primitive
原始多項式 げんしたこうしき, primitive polynomial
容量 ようりょう, content
ガウスの補題 がうすのほだい, Gauss's lemma
ガウスの『整数論』第2章 一次合同式 第42条において整係数ではない有理係数多項式の積が整係数多項式になることはありえないという形で述べられ、証明されている。


