多変数多項式と形式的冪級数
著者:梅谷 武
語句:多変数多項式,多変数形式的冪級数,斉次式,多変数多項式の計算
多変数多項式と形式的冪級数について述べる。
作成:2006-05-18
更新:2021-03-17
多項式という言葉は、本来、係数と不定元の冪乗の積である単項式の和で表される式ということを意味しています。不定元が1個の場合、係数列として定義された一変数多項式が伝統的な多項式と一致することを見ました。それでは不定元が複数個の場合はどのように定義されるのでしょうか。
可換環
R上の不定元が
n個の多項式全体の集合、すなわち
n変数多項式環
R[X1,X2,⋯,Xn]は、次のように帰納的に定義されます。
| R[X1,X2,⋯,Xn] = (R[X1,X2,⋯,Xn-1])[Xn]
|
が可換環であれば
R[X]も可換環ですから、この定義は妥当なものです。しかし、これでは具体的にその元がどのようなものであるかわかりません。そこで不定元が
Xと
Yという2個の場合に、
R[X,Y]が実際にはどのようなものであるかを考えてみましょう。
まず、
R[X]は
{(ai)i∈ℕ | ai∈R}という係数列の集合でした。
R[X,Y]=(R[X])[Y]においては係数が
R[X]ですから、その係数列は
| ((ai0)i∈ℕ,(ai1)i∈ℕ,(ai2)i∈ℕ,⋯)
|
というような係数列の列になります。これは添え字が二重に付いた列
(aij)(i,j) ∈ℕ×ℕとみなせますから、
| R[X,Y] = { (aij)(i,j) ∈ℕ×ℕ | aij ∈R }
|
と考えることができます。このとき、加法と乗法は次のようになります。
Rの任意の元
aは、
| a = | 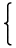 | | |
|
として
R[X,Y]へ埋め込まれます。不定元
X,Yは次のようになります。
| X = | 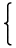 | | | , Y = | 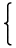 | | |
|
例えば、
ℤ[X,Y]における単項式
3X2Y3は
| 3X2Y3 = | 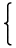 | | |
|
と表現されます。このようにみてくると
R[X,Y]の元は
ℕ×ℕから
Rへの写像を定めていることに気が付きます。
一般に自然数の
n個の直積
ℕnから可換環
Rへの写像で、
0でない値が無限にあるものを
n変数形式的冪級数、
0でない値が有限のものを
n変数多項式、
n変数多項式の中で特に
0でない値が
1個しかないものを
n変数単項式といいます。
n変数形式的冪級数
f,g:ℕn→Rに対して加法と乗法を次のように定義します。
| | | (f+g)((i1,⋯,in)) = f((i1,⋯,in)) + g((i1,⋯,in)) |
|
| | |
| |
∑
(j1,⋯,jn)+(k1,⋯,kn)=(i1,⋯,in) | |
|
|
この加法と乗法によって
n変数多項式の集合は可換環となります。これをを
R上の
n変数形式的冪級数環といいます。特に
0でない値が有限個だけの写像から成る部分集合を
考えると、これは加法と乗法に関して閉じているので部分環になっていますが、これを
R上の
n変数多項式環といいます。
n変数形式的冪級数の不定元を
Xi, i=1,⋯,nで表すことにすれば、単項式は
| aX1k1X2k2 ⋯ Xnkn = | 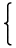 | | |
|
と表すことができ、
n変数形式的冪級数は次のように書くことができます。
∑
(i1,⋯,in)∈ℕn | | a(i1,⋯,in)X1i1X2i2 ⋯ Xnin |
|
|
|
この形式で和と積を書いてみましょう。簡単のために
(i1,⋯,in)を
(i)、
X1i1X2i2 ⋯ Xninを
X(i)と略記することにします。
このように不定元
Xi, i=1,⋯,nで表現する場合、
R上の
n変数形式的冪級数環を
R[[X1,X2,⋯,Xn]]、
n変数多項式環を
R[X1,X2,⋯,Xn]と書きます。このとき
R⊂R[X1,X2,⋯,Xn]⊂R[[X1,X2,⋯,Xn]]という包含関係があります。また、
{ X(i) | (i)∈ℕn }は
R[X1,X2,⋯,Xn]の基底であり、したがって
R[X1,X2,⋯,Xn]は
R-自由加群になっています。
0でない単項式
aX1i1X2i2 ⋯ Xninについて、その次数を
∑k=1nikによって定義します。
0でない多項式についてその次数を、その和に含まれる単項式の次数の最大値として定義し、
deg fと書くことにします。
0でない多項式
fの和に含まれる単項式の次数がすべて
mであるとき、
fを
m次
斉次式せいじしき, homogeneous polynomial、あるいは
m次同次式といいます。次数には次の性質があります。
可換環
R上の
n変数多項式環
R[X1,X2,⋯,Xn]の次数について次が成り立つ。
| (1)
| deg (f+g) ≦ max(deg f,deg g), f,g ∈R[X1,X2,⋯,Xn] |
| (2)
| deg (fg) ≦ deg f + deg g, f,g ∈R[X1,X2,⋯,Xn] |
特に
Rが整域の場合は
(2)で等号が成り立つ。
証明
演習とする。■
多変数多項式は単項式における添え字と係数の組を要素とする連想配列として実装することができます。整係数と有理係数の多変数多項式の加算・減算・乗算・冪乗の計算例を示しておきます。各単項式の
(i1,⋯,in)∈ℕnの後方の
0を省略して書いていることに注意してください。
from PolyM import *
a = PolyM( {(1,1,1):-1, (1,1):3, (1,):-2, (0,1):3, \
(2,6,12):2, ():1 } )
b = PolyM( {(1,):1, ():-5 } )
c = PolyM( {(1,):1 } )
d = PolyM( {():-5 } )
print "a = ", a
print "b = ", b
print "a + b = ", a + b
print "a - b = ", a - b
print "a * b = ", a * b
print "a * b = ", a * c + a * d
print "a^2 = ", a**2
print
PolyM.SetChars( 'stu' )
a = PolyM( {(1,1,1):Fraction(-3,10), (1,1):Fraction(1,25), \
(1,):Fraction(1,4), (0,1):Fraction(1,2), \
(2,6,12):Fraction(-3,10), ():1 } )
b = PolyM( {(1,):1, ():Fraction(-1,2) } )
c = PolyM( {(1,):1 } )
d = PolyM( {():Fraction(-1,2) } )
print "a = ", a
print "b = ", b
print "a + b = ", a + b
print "a - b = ", a - b
print "a * b = ", a * b
print "a * b = ", a * c + a * d
print "a^2 = ", a**2
a = 2X^2Y^6Z^(12) - XYZ + 3XY - 2X + 3Y + 1
b = X - 5
a + b = 2X^2Y^6Z^(12) - XYZ + 3XY - X + 3Y - 4
a - b = 2X^2Y^6Z^(12) - XYZ + 3XY - 3X + 3Y + 6
a * b = 2X^3Y^6Z^(12) - 10X^2Y^6Z^(12) - X^2YZ + 3X^2Y - 2X^2 + 5XYZ - 12XY + 11X - 15Y - 5
a * b = 2X^3Y^6Z^(12) - 10X^2Y^6Z^(12) - X^2YZ + 3X^2Y - 2X^2 + 5XYZ - 12XY + 11X - 15Y - 5
a^2 = 4X^4Y^(12)Z^(24) - 4X^3Y^7Z^(13) + 12X^3Y^7Z^(12) - 8X^3Y^6Z^(12) + 12X^2Y^7Z^(12) + 4X^2Y^6Z^(12) + X^2Y^2Z^2 - 6X^2Y^2Z + 9X^2Y^2 + 4X^2YZ - 12X^2Y + 4X^2 - 6XY^2Z + 18XY^2 - 2XYZ - 6XY - 4X + 9Y^2 + 6Y + 1
a = - 3/10s^2t^6u^(12) - 3/10stu + 1/25st + 1/4s + 1/2t + 1
b = s - 1/2
a + b = - 3/10s^2t^6u^(12) - 3/10stu + 1/25st + 5/4s + 1/2t + 1/2
a - b = - 3/10s^2t^6u^(12) - 3/10stu + 1/25st - 3/4s + 1/2t + 3/2
a * b = - 3/10s^3t^6u^(12) + 3/20s^2t^6u^(12) - 3/10s^2tu + 1/25s^2t + 1/4s^2 + 3/20stu + 12/25st + 7/8s - 1/4t - 1/2
a * b = - 3/10s^3t^6u^(12) + 3/20s^2t^6u^(12) - 3/10s^2tu + 1/25s^2t + 1/4s^2 + 3/20stu + 12/25st + 7/8s - 1/4t - 1/2
a^2 = 9/100s^4t^(12)u^(24) + 9/50s^3t^7u^(13) - 3/125s^3t^7u^(12) - 3/20s^3t^6u^(12) - 3/10s^2t^7u^(12) - 3/5s^2t^6u^(12) + 9/100s^2t^2u^2 - 3/125s^2t^2u + 1/625s^2t^2 - 3/20s^2tu + 1/50s^2t + 1/16s^2 - 3/10st^2u + 1/25st^2 - 3/5stu + 33/100st + 1/2s + 1/4t^2 + t + 1
[
2] ファン・デル・ヴェルデン, 現代代数学〈1〉, 商工出版社, 1959
[
4] 堀田 良之, 岩波講座 現代数学の基礎〈9〉環と体, 岩波書店, 2001
数 学
斉次式 せいじしき, homogeneous polynomial

