有理整数論の基本定理
著者:梅谷 武
語句:クンマー,ヤコビ,素因数分解
素数の特徴付けと有理整数論の基本定理について述べる。
作成:2006-04-24
更新:2021-03-17
この節では整数に関するもっとも基本的な性質について解説します。一般的に整数といったときに、ほとんどの場合は第1章で定義したℤのことを指しますが、数学で整数というときには代数的整数というℤを拡張した概念を指すことがあります。この代数的整数と区別するために普通の整数のことを有理整数と呼んでいます。
次の定理は有理整数における素数概念を特徴付けるものです。これはユークリッド原論第VII巻命題30に相当します。
2以上の整数
pについて、
pが素数であることと
p|ab ⇒ p|a または p|bが成り立つことは同等である。
証明
定理の条件下でpがaを割らないと仮定する。pは素数なので(p,a)=1、すなわちp,aによって生成されるイデアルがℤとなり、xa+yp=1なる整数x,yが存在することがわかる。ここで両辺にbをかけるとxab+ypb=bとなり、p|xab, p|ypbよりp|(xab+ypb)=bとなる。逆にpを2以上の整数としたとき「p|ab ⇒ p|a または p|b」という性質を持てば、もしp=abと書けたとするとa=p,b=1またはa=1,b=pとなりpが素数であることがわかる。■
この定理は一見して当たり前のように思えますが、整数概念を拡張した代数的整数では、例えば
ℤ + ℤ√-5={a + b√-5|a,b∈ℤ}において
2,3,(1+√-5),(1-√-5)はこれ以上分解できませんが、
となり分解の一意性が成り立ちません。また、この環ではイデアル
(2,1+√-5)が単項イデアルになりません。
クンマーKummer, Ernst Eduard,1810-1893は
ℤ[ζp]上で整数論を展開することについて研究し、この上で素因数分解の一意性が成り立てば有名なフェルマーの大定理が証明できることに気が付きました。そこでフェルマーの問題を解決したという論文を投稿しましたが、
ヤコビJacobi, Carl Gustav Jacob, 1804-1851に誤りを指摘されて取り下げたという逸話が残っています。クンマーが1844年4月20日付けでベルリン学士院に送ったこの原稿は、近年、H.M.Edwardsによって発見されています。
次の定理がこの節の目的となるものです。ガウスは『整数論』第2章一次合同式の冒頭でユークリッド原論第VII巻命題30を復習した後にこの定理を証明し、以後の議論の基礎としています。
証明
0でない整数
nを与える。
±1は
nの正負に対応して定まるので
nを正として議論を進める。
n=1のときは
0個の素数の積と考える。
nが素数の積に分解されることを
nに関する数学的帰納法で証明する。
n=2とする。
2は素数でありこれ以上分解することはできない。
nまで素因数分解されたと仮定して
n+1について考える。
n+1が素数であれば、それ以上は分解できない。合成数であれば
n+1=abと約数の積で表すことができるが、帰納法の仮定により
a,bはそれぞれ素数に分解されているから
n+1も素数の積に分解される。
nが次のように2通りに素因数分解されたとする。
| n = p1p2 ⋯ pr = q1q2 ⋯ qs, 0≦r≦s
|
このときどの
piも
pi|q1q2 ⋯ qsであるから、いずれかの
qjに対して
pi|qjとなり、両方とも素数なので
pi=qjとなり、
r=sである。■
次の系はユークリッド原論第IX巻命題20に相当します。
証明
素数が有限であると仮定して、それらをすべてかけて1を加えた数
を考える。これをどの素数
piで割っても
1が余るので、
aの素因数分解にはどの
piも含まれない。これは矛盾である。したがって素数は無限にある。■
整数
nの素因数分解を積の記号
∏を使って次のように書くことにします。
| n = ± ∏p:素数{pep(n)} = ± p1ep1(n) p2ep2(n) ⋯ prepr(n)
|
この式で
ep(n)は素数
pの
nの素因数分解における指数を表します。積はすべての素数にわたりますから、いわゆる無限積になりますが、指数が
0でないのは有限個ですから実際には有限個の積です。
任意の自然数
a,bが与えられたとき、その素因数分解を
| a = ∏p:素数 pep(a), b = ∏p:素数 pep(b)
|
とする。このとき
となる。ここで、任意の整数
s,tについて
| max(s,t) = | 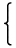 | | | ,
min(s,t) = | 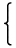 | | |
|
としている。この結果、次式が成り立つ。
証明
max(s,t)+min(s,t)=s+tより直ちに従う。■
[
1] 中村幸四郎, 伊東俊太郎, 寺阪英孝, 池田美恵 訳,
ユークリッド原論, 共立出版, 1996
人 物
クンマー Kummer, Ernst Eduard,1810-1893
ドイツの数学者。数論
ヤコビ Jacobi, Carl Gustav Jacob, 1804-1851
ドイツの数学者。数論・楕円関数論。
数 学
素因数分解 そいんすうぶんかい, prime factorization


