自然数の場合と同様に二つの整数a,b(≠0)がある整数qによってa=bqと表されるとき、aはbの倍数ばいすう, multipleである、あるいはbはaの約数やくすう, divisorであるといい、b|aと書くことにします。この二つの整数のちょうど割れるか割れないかという関係を整除関係といいます。この節では整除関係の基本的な性質について調べてみます。

 まず、任意の整数aについてa=1×a、0=0×aですから、 であることがわかります。次にa|b,b|cとするとb=aq,c=bq'と書けるのでc=aqq'となり、a|cであることがわかります。したがって、 が成り立ちます。さらにa|b,b|aであるとしましょう。割る側は0でないと仮定していますからa≠0,b≠0であることに注意してください。b=aq,a=bq'よりa=aqq'となりqq'=1ですからq=q'=±1となります。したがって、 が成り立ちます。整数a,bがa|bかつb|aという条件を満たすときaとbは同伴どうはん, associatedであるといい、a⋍bと書くことにします。 これはb=±aと同じことです。同伴関係を⋍で表すと、 上で述べたことは、同伴関係は整数ℤ上の同値関係であって、その同値類全体の集合ℤ/⋍において整除関係|が順序関係になっていると言い換えることができます。この同値類の代表として正の数をとることにすれば、ℤ/⋍は自然数の集合ℕと1対1に対応します。このことを命題の形で整理しておきましょう。

 b|aであれば－b|aですから、約数という概念は同伴類に対して定まるものであることがわかります。ですから整数aの約数全体の集合を考えるときに、整数全体の集合ℤではなくて、その同伴類の集合ℤ/⋍を考えるのが自然です。さらにℤ/⋍は自然数の集合ℕと1対1に対応しますから、今後は簡単のために自然数の部分集合である正の約数全体の集合だけを考えることにしましょう。整数aの正の約数全体の集合をD(a)で表すことにします。例えば12と15の場合、次のようになります。 整数aの任意の正の約数dについて0＜d≦aが成り立ちますから、D(a)は有限集合です。2以上の整数pでD(p)={1,p}となるとき、すなわち正の約数が1と自分自身しかないときにpを素数そすう, prime numberといいます。素数でない数を合成数ごうせいすう, composite numberといいます。

 整数d(≠0)が二つの整数a,bについてd|a,d|bとなっているときdをa,bの公約数こうやくすう, common divisorであるといいます。a,bの正の公約数全体の集合はD(a)∩D(b)と一致します。その集合の最大の数、すなわちaとbの公約数の中で最大のものをaとbの最大公約数さいだいこうやくすう, greatest common divisorといい、gcd(a,b)あるいは単に(a,b)と書くことにします。例えば12と15の場合、 ですから、gcd(12,15)=3となります。gcd(a,b)=1のときaとbは互いに素であるといいます。

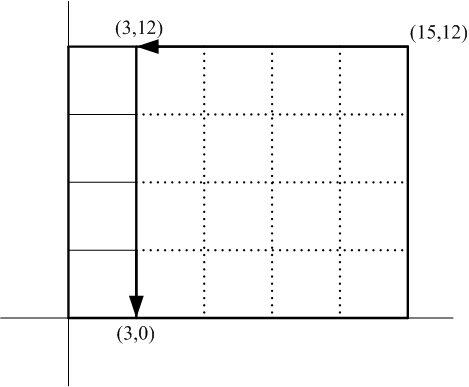
 図に示すように二つの整数a,bの最大公約数を求めるという問題は辺の長さがa,bである長方形の領域を同じ大きさの正方形のタイルで埋め尽くすときに正方形の辺の長さの最大値を求めるという幾何学の問題に置き換えることができます。

 ユークリッド原論の第VII巻命題２に二つの整数の最大公約数を求める算法が解説されています。この算法はユークリッドの互除法ゆーくりっどのごじょほう, Euclidean algorithmと呼ばれています。現代においても整数の計算のみならず多項式の計算においても簡単でとても効率がよい算法として重宝されているものです。

 これで最大公約数が求まることは、d∈D(a)∩D(b)とするとd|r(=a－bq)であり、d'∈D(b)∩D(r)とするとd'|a(=bq+r)となることから、 となり、公約数の集合が一致することと繰り返しの際に変数a,bがとも前回よりも小さくなるのでいつかはr=0となることからわかります。

 図の例にこれを当てはめてみましょう。 幾何学的な言葉で表現すれば、長方形から短い辺の正方形を取れるだけ取り去り、残りがまた長方形であれば同じことを繰り返し、残りがなくなったときの辺の長さが最大公約数であるということになります。これをプログラミングしてみます。

sample2.2.5.py

def gcd( a, b ):
  while b != 0:
    r = a % b
    a = b
    b = r
  if a < 0:
    return -a
  else:
    return a
 
a = 9749560641517
b = 8770036831691
d = gcd( a, b )
print 'gcd( %d, %d ) = %d' % ( a, b, d )

sample2.2.5.pyの実行結果

gcd( 9749560641517, 8770036831691 ) = 6972593

sample2.2.5.rb

def gcd(a, b)
  while b != 0
    r = a % b
    a = b
    b = r
  end
  if a < 0
    return -a
  else
    return a
  end
end
 
a = 9749560641517
b = 8770036831691
d = gcd(a, b)
printf "gcd(%d, %d) = %d", a, b, d

sample2.2.5.rbの実行結果

gcd(9749560641517, 8770036831691) = 6972593

参考文献