2.1 四元数

著者:梅谷武
語句:四元数,スカラー,ベクトル,共役,テンソル,三次元単位球面,ベルソル,ベクトル比,比例,極形式

古典幾何を基礎とするハミルトン流の四元数論をなるべく忠実に再現する。ハミルトンの記法にはやや違和感があるが、演算子を被演算子の前に記述するいわゆるポーランド記法であり、プログラミング言語で扱いやすいためそのまま踏襲する。

作成:2010-05-31
更新:2021-04-25

アフィン空間(U,V³)、V³の正規直交基底(i,j,k)、アフィン標構(O;i,j,k)が与えられているとして議論を進める。

実線形空間としての直和ℍ := ℝ⊕V³について考える。ℍの元を四元数しげんすう, quaternionと呼び、a,b,cのように太字の英小文字で表す。ℝの元をスカラーすからー, scalarと呼び、x,y,zのように標準の英小文字で表す。V³の元をベクトルべくとる, vectorと呼び、α,β,γのようにギリシャ小文字で表す。

任意の四元数qをスカラーとベクトルの組として次のように表現する。

q = w + α, w ∈ ℝ, α ∈ V³

α=(x,y,z)と座標表現する場合は、

q = w + xi + yj + zk

と記す。

自然な射影S,Vが次のように定義される。

S:ℍ → ℝ, q = w + α ↦ Sq = w

V:ℍ → V³, q = w + α ↦ Vq = α

共役きょうやく, conjugateKを次のように定義する。

K:ℍ → ℍ, q = w + α ↦ Kq = w - α

四元数q = [w, (x,y,z)]のノルムを

:= √w² + x² + y² + z²

で定義することにより、ℍはノルム空間となる。ハミルトン流では、ノルムをテンソルてんそる, tensorTと呼ぶ。

T:ℍ → ℝ⁺, q ↦ Tq =

大きさが1の四元数全体

S³ := { q ∈ ℍ ∣ Tq = 1 }

を三次元単位球面さんじげんたんいきゅうめん, 3 dimensional unit sphereと呼ぶ。

ベルソルべるそる, versorUを次のように定義する。

U:ℍ^× → S³, q ↦ Uq =

命題2.1.1.9 射影演算子

q∈ℍ, w∈ℝ, α∈V³について次が成り立つ。

Sq + Vq

q - Vq

q - Sq

Sq - Vq

Sα

Vα

α, β ∈ V³について、その四元数としての積を次のように定義する。

αβ := - 〈α,β〉 + α × β

これは射影演算子を使うと次のように表現できる。

(2.9)

Sαβ

- 〈α,β〉

(2.10)

Vαβ

α × β

内積は対称性をもち、ベクトル積は交代性をもつことから次が成り立つ。

(2.11)

Sαβ

Sβα

(2.12)

Vαβ

- Vβα

これは次のように式変形できる。

(2.13)

αβ + βα

2Sαβ

(2.14)

αβ - βα

2Vαβ

α∥βのとき、β = rα, r∈ℝと書けば、

αβ = - r〈α,α〉 = -r(Tα)²

α⊥βのとき、

αβ = α × β

零でないベクトルαについて、

(Tα)²

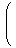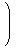= 1

が成り立つことから、積に関する逆元は次のようなベクトルになる。

(2.15)

= α^-1 = -

(Tα)²

= -

Uα

Tα

命題2.1.2.8 結合律

α,β,γ∈V³について次が成り立つ。

(2.16)

(αβ)γ = α(βγ)

2.1.3 四元数の積

ベクトル空間V³の正規直交基底間の積は次の性質を満たす。

(2.17)

i² = j² = k² = ijk = - 1

(2.18)

ij = -ji = k

(2.19)

jk = -kj = i

(2.20)

ki = -ik = j

一般の四元数の積は分配律が成り立つように定義する。a,b ∈ ℍを

a = w₁ + x₁ i + y₁ j + z₁ k, w₁,x₁,y₁,z₁ ∈ ℝ

b = w₂ + x₂ i + y₂ j + z₂ k, w₂,x₂,y₂,z₂ ∈ ℝ

と表現すると、

a b

(w₁ + x₁ i + y₁ j + z₁ k) (w₂ + x₂ i + y₂ j + z₂ k)

(w₁w₂ - x₁x₂ - y₁y₂ - z₁z₂) + (w₁x₂ + x₁w₂ + y₁z₂ - z₁y₂)i

(w₁y₂ - x₁z₂ + y₁w₂ + z₁x₂)j + (w₁z₂ + x₁y₂ - y₁x₂ + z₁w₂)k

上のaに対して、その共役Kaは

Ka = w₁ - x₁ i - a₂ j - z₁ k

となるから

a Ka

(w₁² + x₁² + y₁² + z₁²) + (-w₁x₁ + x₁w₁ - y₁z₁ + z₁y₁)i

(-w₁y₁ - x₁z₁ + y₁w₁ - z₁x₁)j + (-w₁z₁ - x₁y₁ + y₁x₁ + z₁w₁)k

w₁² + x₁² + y₁² + z₁² = (Ta)²

によりaの逆元が求まる。

(2.21)

a^-1 =

(Ta)²

UKa

命題2.1.3.4 多元環

四元数ℍはℝ上の多元環であり、0でない元は単元である。特に結合律を満たすが、可換律は満たさない。

命題2.1.3.6 積のテンソル

四元数a,bについて、次が成り立つ。

(2.23)

Tab = TaTb

2.1.4 ベクトル比と平面比例

零でない二つのベクトルα,β∈V³の商

= β α^-1

はベクトル比べくとるひ, vector ratio

β : α

として幾何学的な意味をもっている。ここではこれに関する幾何学的考察を行なう。

四元数の積が可換でないことから、

β α^-1 ≠ α^-1β,

≠

δβ

γα

であることに注意しなければならない。ベクトル比の合成を計算するにあたっては通常の算術的直感を排除する必要がある。

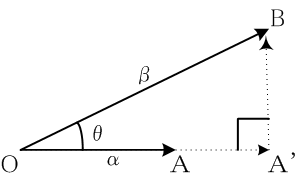
図2.1.4.3 ベクトル比

ベクトル比β:α, α∦βが与えられたとき、二つのベクトルを原点Oを始点とする有向線分で描き、αからβへ反時計回りに向う角度θがπより小さくなるように、α,βによって生成される平面を紙面と一致させる。

[OB]

[OA]

[OA'] + [A'B]

[OA]

[OA']

[OA]

[A'B]

[OA]

Tβ cosθ

Tα

Tβ sinθ

Tα

∙ UV

cosθ

sinθ

∙

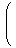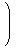ここで、UVβ/αは紙面垂直上方に向うベルソルであり、β/αの軸と呼ばれる。最後の極形式表現により、ベクトル比はこの軸と角度θ、線長比Tβ/Tαによってのみ定まることがわかる。以後、角度θを

∠

と書くことにする。

命題2.1.4.5 ベクトル比の比例

二つのベクトル比が比例ひれい, proportionすることは、各ベクトル比を構成する二つのベクトルが生成する三角形が、同一平面上にあり向きを含めて相似であることと同等である。

次にベクトル比が引き起こす変換について考える。

補題2.1.4.7

零でない二つのベクトルα,β∈V³, α∦βが与えられたとき、βαβ^-1はα,βによって生成されるV³内の平面上、αのβを含む直線に関する鏡像になっている。

証明

Sβαβ^-1 = Sαβ^-1β = Sα = 0よりβαβ^-1はベクトルであり、Tβαβ^-1 = TβTαTβ^-1 = Tαより長さが等しく、

βαβ^-1 + α = β(αβ^-1 + β^-1α) = β ∙ 2Sαβ^-1

より、βαβ^-1はα,βによって生成される平面上にあり、Sβαβ^-1β=Sβα=Sαβより、βに対する角度が等しいことから結論が従う。■

補題2.1.4.9

零でない二つのベクトルα,β∈V³, α∦βが与えられたとき、その比β:αはα,βによって生成されるV³内の平面上のαをβに写す線形変換を引き起こす。またこの平面上にないベクトルγの像(β:α) γはベクトルにはならない。

証明

(sα + tβ) = sβ + t

(Tβ)²

(Tα)²

βαβ^-1, s,t ∈ ℝ

■

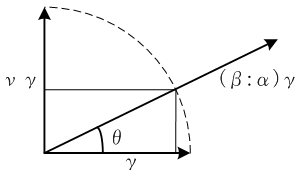
ベクトル比β:α, α∦βが与えられたとき、それを極形式表現し、その軸をν = UVβ/α、角度をθ = ∠ β/α、大きさをr = Tβ/αとおく。

= r(cosθ + sinθ ∙ ν)

垂直上方向の軸νに垂直な平面上の任意のベクトルγにそのベクトル比を左から作用させる。

r(cosθ + sinθ ∙ ν) γ

r(cosθ ∙ γ + sinθ ∙ νγ)

νγはνを軸としてγを90度回転させたものであるから、この作用はγを軸νに関して反時計回りにθだけ回転させてr倍の伸縮を行なう、この平面上の向きを変えない相似変換である。

図2.1.4.12 ベクトル比の左からの作用

命題2.1.4.13 ベクトル比の左からの作用

ベクトル比の左からの作用は、その軸νに垂直な平面上で反時計回りにθの回転とr倍の伸縮の向きを変えない相似変換を引き起こす。

軸νに垂直な平面上の任意のベクトルγにそのベクトル比を右から作用させる。

= r(cosθ ∙ γ + sinθ ∙ γν)

γν = - νγであるから、回転が時計回りになる。

命題2.1.4.15 ベクトル比の右からの作用

ベクトル比の右からの作用は、その軸νに垂直な平面上で時計回りにθの回転とr倍の伸縮の向きを変えない相似変換を引き起こす。

ベクトル比の共役を左から作用させると

γ = r(cosθ ∙ γ + sinθ ∙ -νγ)

となり右からの作用と同じ変換になる。

命題2.1.4.17 ベクトル比の共役の左からの作用

ベクトル比の共役の左からの作用は、その軸νに垂直な平面上で時計回りにθの回転とr倍の伸縮の向きを変えない相似変換を引き起こす。

共役の右からの作用は左からの作用と同じ変換になる。

命題2.1.4.19 ベクトル比の共役の右からの作用

ベクトル比の共役の右からの作用は、その軸νに垂直な平面上で反時計回りにθの回転とr倍の伸縮の向きを変えない相似変換を引き起こす。

最後に任意の零でなくスカラーでもない四元数qがベクトル比として表されることを示す。

q = TqUq

ここで、ベルソルUqを次のように書くことができる。

Uq = a + b ∙ ν, a² + b² = 1, b > 0, Tν = 1

ここで、ベルソルν = UVqはbを正にする条件により一意的に定まる。このとき、0 < θ < πなるθ = ∠qが一意的に定まり、

cos∠q + sin∠qUVq

と書くことができる。したがって、

q = Tq(cos∠q + sin∠qUVq)

と極形式に表現することができる。

命題2.1.4.21 四元数の極形式表現

零でない四元数q∈ℍ^×は次のように極形式きょくけいしき, polar formで一意的に表現することができる。

q = Tq(cos∠q + sin∠qUVq), ∠q ∈ [0,π]

軸UVqに垂直な平面上のベクトルαを任意に選び、それを∠qだけ回転させて、 Tq倍の伸縮を行なった結果をβとすれば、

q =

と書くことができる。

零でないスカラーを平行なベクトル比と考えれば次のように主張することができる。

命題2.1.4.24 四元数はベクトル比

零でない四元数はベクトル比である。

2.1.5 参考文献

[1] 梅谷武, 幾何学事始, pisan-dub.jp, 2009

[2] W.R.Hamilton, Elements on quaternions, Longmans, Green, & Co., London, 1866

[3] A.S.Hardy, Elements on quaternions, 1891

[4] Charles Jasper Joly, A manual of quaternions, Franklin Classics, 1905(2018)

数　　学

四元数しげんすう, quaternion
スカラーすからー, scalar
ベクトルべくとる, vector
共役きょうやく, conjugate
テンソルてんそる, tensor
三次元単位球面さんじげんたんいきゅうめん, 3 dimensional unit sphere
ベルソルべるそる, versor
ベクトル比べくとるひ, vector ratio
比例ひれい, proportion
極形式きょくけいしき, polar form

Published by SANENSYA Co.,Ltd.