2.3節 正多面体
著者:梅谷 武
語句:正多面体, 対称変換群, 合同変換群の有限部分群
正多面体の対称変換群を決定し、正四面体・立方体の対称変換群を群論的作図法で可視化する。
作成:2010-01-18
更新:2021-07-01
2.3 正多面体
2.3.1 正多面体の対称性
 前節の議論により、正多面体の対称変換群は直交群の有限部分群であり、対称群に埋め込むことができます。ここでは五種類の正多面体の内、正四面体と立方体の対称変換群の構造を決定し、それを視覚的に示します。
2.3.2 正四面体の対称変換群
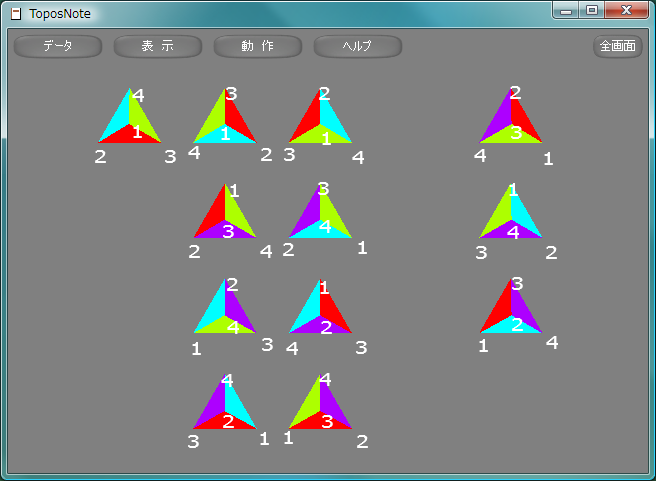
 正四面体の対称変換で回転で表現できるものは、重心と頂点を結ぶ４本の軸に関する回転と二組の頂点対に関する互換の積です。これらは位数12の群を成し、交代群A4と同型になります。そのすべてを図示します。
算譜2.3.2.2 sample204.lua
package.path = "std/?.lua"
require( "Geometry" )
 
a = math.sqrt( 6.0 ) / 2.0
b = math.sqrt( 3.0 ) / 3.0
c = math.sqrt( 6.0 ) / 6.0
d = 2.0 * b
vertices = {
  0.0,  a, 0.0, 0.0, 1.0, 0.0, 0.0, 0.0,
 -1.0, -c,  -b, 0.0, 1.0, 0.0, 0.0, 0.0,
  1.0, -c,  -b, 0.0, 1.0, 0.0, 0.0, 0.0,
  0.0, -c,   d, 0.0, 1.0, 0.0, 0.0, 0.0
}
function tetrahedron()
  dxSetRenderState( D3DRS_CULLMODE, D3DCULL_NONE )
  dxSetColorHSV(   0.0, 1.0, 1.0 )
  dxTriangleMesh( 4, vertices, 1, { 0, 1, 2 } )
  dxSetColorHSV(  90.0, 1.0, 1.0 )
  dxTriangleMesh( 4, vertices, 1, { 0, 2, 3 } )
  dxSetColorHSV( 180.0, 1.0, 1.0 )
  dxTriangleMesh( 4, vertices, 1, { 0, 3, 1 } )
  dxSetColorHSV( 270.0, 1.0, 1.0 )
  dxTriangleMesh( 4, vertices, 1, { 1, 3, 2 } )
  dxPrint( 0.0+0.1,  a+0.1, 0.0+0.1, 1.0, 1.0, 1.0, "1" )
  dxPrint(-1.0-0.1, -c-0.1,  -b-0.1, 1.0, 1.0, 1.0, "2" )
  dxPrint( 1.0+0.1, -c-0.1,  -b-0.1, 1.0, 1.0, 1.0, "3" )
  dxPrint( 0.0+0.1, -c-0.1,   d+0.1, 1.0, 1.0, 1.0, "4" )
  dxSetRenderState( D3DRS_CULLMODE, D3DCULL_CCW )
end
Tetrahedron = Figure.new( function()
  tetrahedron()
end )
E = Transformation.new( function()
end )
R1 = Transformation.new( function()
  Rotate( 120.0, 0.0, 0.0, 1.0 )
end )
R2 = Transformation.new( function()
  Rotate( 120.0, -1.0, -b, -c )
end )
R3 = Transformation.new( function()
  Rotate( 120.0,  1.0, -b, -c )
end )
R4 = Transformation.new( function()
  Rotate( 120.0,  0.0,  d, -c )
end )
T1 = Transformation.new( function()
  Translate( 3.0, 0.0, 0.0 )
end )
T2 = Transformation.new( function()
  Translate( 0.0,-3.0, 0.0 )
end )
 
draw =                           E * Tetrahedron
draw =                 ( T1 * R1 ) * Tetrahedron
draw =             ( T1^2 * R1^2 ) * Tetrahedron
draw =            ( T1 * T2 * R2 ) * Tetrahedron
draw =        ( T1^2 * T2 * R2^2 ) * Tetrahedron
draw =          ( T1 * T2^2 * R3 ) * Tetrahedron
draw =      ( T1^2 * T2^2 * R3^2 ) * Tetrahedron
draw =          ( T1 * T2^3 * R4 ) * Tetrahedron
draw =      ( T1^2 * T2^3 * R4^2 ) * Tetrahedron
draw =        ( T1^4 * R2^2 * R1 ) * Tetrahedron
draw =   ( T1^4 * T2 * R4^2 * R2 ) * Tetrahedron
draw = ( T1^4 * T2^2 * R2^2 * R3 ) * Tetrahedron
 
tnNewObject()
図2.3.2.3 sample204.lua
sample204.lua
 これ以外の対称変換は鏡映と回転の積で表現されます。

定理2.3.2.5 正四面体の対称変換群

正四面体の対称変換群をTetraで表すと、
Tetra ≅ S4
Tetra ∩ SO(3) ≅ A4
2.3.3 立方体の対称変換群
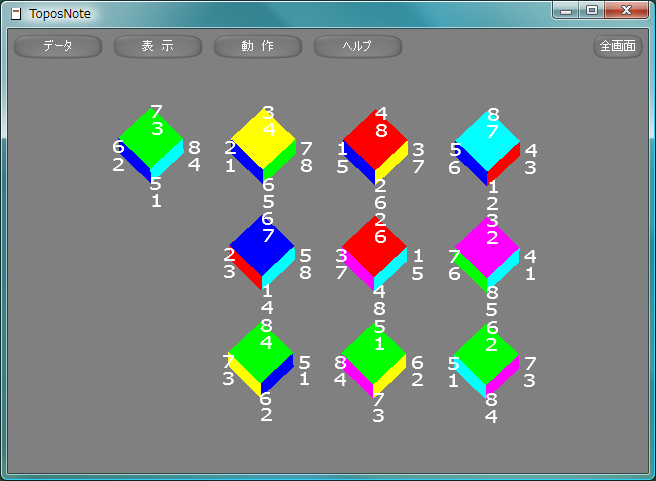
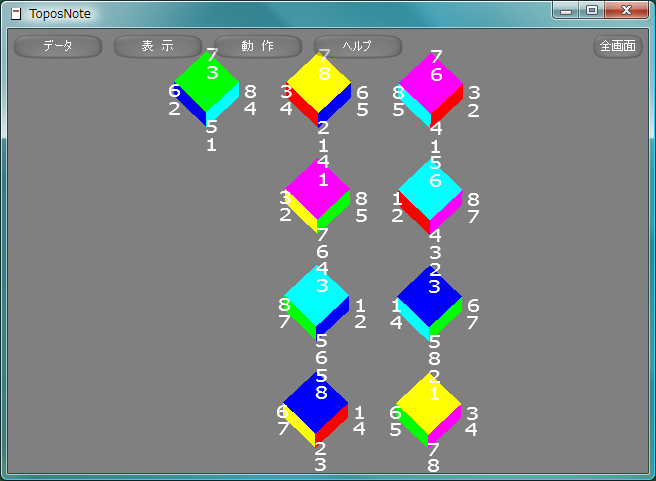
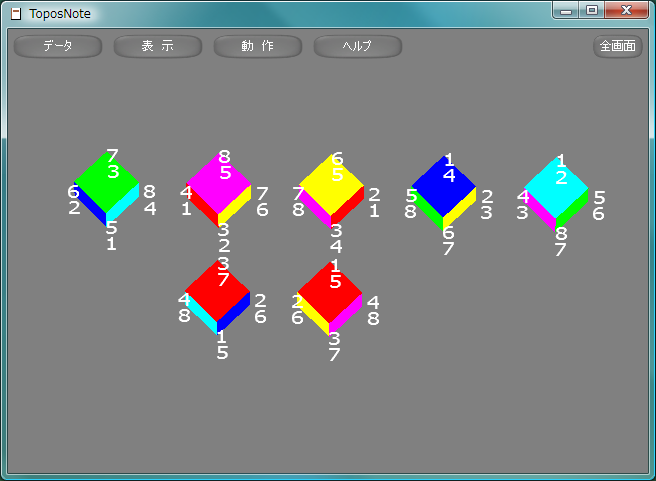
 立方体の対称変換で回転で表現できるものは、４本の対角線の置換として表現するができて、そのすべての組み合わせに対応する回転が存在することから、対称群S4に同型であることがわかります。そのすべてを図示します。
算譜2.3.3.2 sample205a.lua
package.path = "std/?.lua"
require( "Geometry" )
 
a = math.sqrt( 3.0 ) / 3.0
vertices = {
 -a,  -a,  -a,  -a,  -a,  -a, 0.0, 0.0,
 -a,  -a,   a,  -a,  -a,   a, 0.0, 0.0,
  a,  -a,   a,   a,  -a,   a, 0.0, 0.0,
  a,  -a,  -a,   a,  -a,  -a, 0.0, 0.0,
 -a,   a,  -a,  -a,   a,  -a, 0.0, 0.0,
 -a,   a,   a,  -a,   a,   a, 0.0, 0.0,
  a,   a,   a,   a,   a,   a, 0.0, 0.0,
  a,   a,  -a,   a,   a,  -a, 0.0, 0.0
}
function cube()
  dxSetRenderState( D3DRS_CULLMODE, D3DCULL_NONE )
  dxSetColorHSV(   0.0, 1.0, 1.0 )
  dxTriangleMesh( 8, vertices, 2, { 0, 1, 2, 0, 2, 3 } )
  dxSetColorHSV(  60.0, 1.0, 1.0 )
  dxTriangleMesh( 8, vertices, 2, { 1, 5, 6, 1, 6, 2 } )
  dxSetColorHSV( 120.0, 1.0, 1.0 )
  dxTriangleMesh( 8, vertices, 2, { 5, 4, 7, 5, 7, 6 } )
  dxSetColorHSV( 180.0, 1.0, 1.0 )
  dxTriangleMesh( 8, vertices, 2, { 4, 0, 3, 4, 3, 7 } )
  dxSetColorHSV( 240.0, 1.0, 1.0 )
  dxTriangleMesh( 8, vertices, 2, { 0, 4, 5, 0, 5, 1 } )
  dxSetColorHSV( 300.0, 1.0, 1.0 )
  dxTriangleMesh( 8, vertices, 2, { 2, 6, 7, 2, 7, 3 } )
  dxPrint( -a-0.1, -a-0.1, -a-0.1, 1.0, 1.0, 1.0, "1" )
  dxPrint( -a-0.1, -a-0.1,  a+0.1, 1.0, 1.0, 1.0, "2" )
  dxPrint(  a+0.1, -a-0.1,  a+0.1, 1.0, 1.0, 1.0, "3" )
  dxPrint(  a+0.1, -a-0.1, -a-0.1, 1.0, 1.0, 1.0, "4" )
  dxPrint( -a-0.1,  a+0.1, -a-0.1, 1.0, 1.0, 1.0, "5" )
  dxPrint( -a-0.1,  a+0.1,  a+0.1, 1.0, 1.0, 1.0, "6" )
  dxPrint(  a+0.1,  a+0.1,  a+0.1, 1.0, 1.0, 1.0, "7" )
  dxPrint(  a+0.1,  a+0.1, -a-0.1, 1.0, 1.0, 1.0, "8" )
  dxSetRenderState( D3DRS_CULLMODE, D3DCULL_CCW )
end
Cube = Figure.new( function()
  cube()
end )
E = Transformation.new( function()
end )
R1 = Transformation.new( function()
  Rotate( 90.0, 1.0, 0.0, 0.0 )
end )
R2 = Transformation.new( function()
  Rotate( 90.0, 0.0, 1.0, 0.0 )
end )
R3 = Transformation.new( function()
  Rotate( 90.0, 0.0, 0.0, 1.0 )
end )
T1 = Transformation.new( function()
  Translate( 2.0,-2.0, 0.0 )
end )
T2 = Transformation.new( function()
  Translate(-2.0,-2.0, 0.0 )
end )
 
draw =                      E * Cube
draw =            ( T1 * R1 ) * Cube
draw =        ( T1^2 * R1^2 ) * Cube
draw =        ( T1^3 * R1^3 ) * Cube
draw =       ( T1 * T2 * R2 ) * Cube
draw =   ( T1^2 * T2 * R2^2 ) * Cube
draw =   ( T1^3 * T2 * R2^3 ) * Cube
draw =     ( T1 * T2^2 * R3 ) * Cube
draw = ( T1^2 * T2^2 * R3^2 ) * Cube
draw = ( T1^3 * T2^2 * R3^3 ) * Cube
 
tnNewObject()
図2.3.3.3 sample205a.lua
sample205a.lua
算譜2.3.3.4 sample205b.lua
R4 = Transformation.new( function()
  Rotate( 120.0, a, a, a )
end )
R5 = Transformation.new( function()
  Rotate( 120.0, a,-a, a )
end )
R6 = Transformation.new( function()
  Rotate( 120.0,-a,-a, a )
end )
R7 = Transformation.new( function()
  Rotate( 120.0,-a, a, a )
end )
T1 = Transformation.new( function()
  Translate( 2.0,-2.0, 0.0 )
end )
T2 = Transformation.new( function()
  Translate(-2.0,-2.0, 0.0 )
end )
 
draw =                      E * Cube
draw =            ( T1 * R4 ) * Cube
draw =        ( T1^2 * R4^2 ) * Cube
draw =       ( T1 * T2 * R5 ) * Cube
draw =   ( T1^2 * T2 * R5^2 ) * Cube
draw =     ( T1 * T2^2 * R6 ) * Cube
draw = ( T1^2 * T2^2 * R6^2 ) * Cube
draw =     ( T1 * T2^3 * R7 ) * Cube
draw = ( T1^2 * T2^3 * R7^2 ) * Cube
図2.3.3.5 sample205b.lua
sample205b.lua
算譜2.3.3.6 sample205c.lua
R8 = Transformation.new( function()
  Rotate( 180.0, a, 0.0, a )
end )
R9 = Transformation.new( function()
  Rotate( 180.0, 0.0, a, a )
end )
Ra = Transformation.new( function()
  Rotate( 180.0,-a, 0.0, a )
end )
Rb = Transformation.new( function()
  Rotate( 180.0, 0.0,-a, a )
end )
Rc = Transformation.new( function()
  Rotate( 180.0, a, a, 0.0 )
end )
Rd = Transformation.new( function()
  Rotate( 180.0,-a, a, 0.0 )
end )
T1 = Transformation.new( function()
  Translate( 2.0,-2.0, 0.0 )
end )
T2 = Transformation.new( function()
  Translate(-2.0,-2.0, 0.0 )
end )
 
draw =                  E * Cube
draw =        ( T1 * R8 ) * Cube
draw =      ( T1^2 * R9 ) * Cube
draw =      ( T1^3 * Ra ) * Cube
draw =      ( T1^4 * Rb ) * Cube
draw =   ( T1 * T2 * Rc ) * Cube
draw = ( T1^2 * T2 * Rd ) * Cube
図2.3.3.7 sample205c.lua
sample205c.lua
 これ以外の対称変換は鏡映と回転の積で表現されます。

定理2.3.3.9 立方体の対称変換群

立方体の対称変換群をCube、鏡映群をRef(3)で表すと、
Cube ≅ Ref(3) × S4
Cube ∩ SO(3) ≅ S4
2.3.4 正八面体の対称変換群
 下図のように正八面体を立方体に内接させると、正八面体の頂点と立方体の面、正八面体の面と立方体の頂点が１対１に対応します。この性質から、正八面体と立方体の対称変換群は同じものであることがわかります。
 sample206.lua
動画2.3.4.3 sample206.lua

定理2.3.4.4 正八面体の対称変換群

正八面体の対称変換群をOctaで表すと、
Octa ≅ Cube
2.3.5 正十二面体の対称変換群
 正十二面体は、正八面体と立方体の対応と同じように正二十面体と対応します。
 sample207.lua
動画2.3.5.3 sample207.lua

定理2.3.5.4 正十二面体の対称変換群

正十二面体の対称変換群をDodeca、正二十面体の対称変換群をIcosaで表すと、
Dodeca ≅ Icosa
2.3.6 正二十面体の対称変換群
 正二十面体の対称変換群の構造を決定し、それを視覚的に表現することはかなり長くなるので現段階では省略し、結果だけを記しておきます。これについては参考文献[4]を参照してください。

定理2.3.6.2 正二十面体の対称変換群

Icosa ≅ Ref(3) × A5
Icosa ∩ SO(3) ≅ A5

証明

略■

定理2.3.6.4 合同変換群の有限部分群の分類

合同変換群の有限部分群は巡回群、正二面体群、そして正多面体の対称変換群に限る。

証明

略■
2.3.7 参考文献
[1] 梅谷 武, 幾何学事始, pisan-dub.jp, 2009
[2] H.S.M. コクセター, 幾何学入門(上), ちくま学芸文庫, 2009
img
 
 
[3] H.S.M. コクセター, 幾何学入門(下), ちくま学芸文庫, 2009
img
 
 
[4] Elmer G. Rees, 幾何学講義, 共立出版, 1992
img
 
 
[5] 志賀 浩二, 群論への30講, 朝倉書店, 1989
img
 
 
[6] 原田 耕一郎, 群の発見, 岩波書店, 2001
img
 
 
Published by SANENSYA Co.,Ltd.