はしがき
著者:梅谷 武
『幾何学事始』の由来と内容の概説。
作成:2009-09-28
更新:2021-03-28
更新:2021-03-28
リンク切れを次のような方針で修正しました。
- 参考文献のスポンサーサイトへのリンクのみ有効。
- 絶版になっているものはリンク無しで書誌情報のみ記載。
- 出版形態が変化しているものは新しい形態へ変更。
- 10年間リンクが変更されていない公的サイトへのリンクは有効。
- 個人サイトへのリンクは削除。
つい最近まで、エウクレイデスEuclides(英語名:ユークリッドEuclid)の『原論』を読むのは、数学史を研究するごく少数の人々に限られていました。数学を学ぼうとする人であれば『原論』ではなく、ヒルベルトDavid Hilbert, 1862-1943の『幾何学基礎論』を選ぶのが普通でしょう。どうせ幾何学の基礎を学ぶのであれば、ヒルベルトによって否定された体系ではなく、現代的な体系を学んだ方が学習効率がいいに決まっていると考えるのが自然です。
私の場合も、幾何学を学ぶための基礎として『原論』を読もうとしたことはありませんでした。5年ほど前に量の理論について調べているときに、量について語る人の多くがユークリッドに言及しているということに気が付いて、量の問題を考えるための素材として『原論』を原典で読んでおこうとしたのが最初です。今から考えるとこのアプローチはまったく偶然のことながら、現代人が『原論』を読むときの壺を突いているものでした。もしこのルートで登らなければ、『原論』という忘れられた名峰を登攀するためのガイドブックを書こうとは思わなかったでしょう。
とはいっても私自身もまだ頂上に到達したわけではありません。5合目にたどり着いて一休みしているところです。そして雲の切れ間からやっとこの山の全貌が見えてきて、現在の装備ではとても頂上までは登れないということがわかり、一旦下山して、これまでに得た情報からより安全で確実性の高い登山計画を立案し、装備を整えて再び挑戦しようとしているというのが現状です。
本書はその登山計画案の前半をまとめたものです。
エウクレイデスの生涯や『原論』の成立についての正確なところはほとんどわかっておらず、数多くの伝承から、その全体像をおぼろげに推察することしかできません。ここでは、これらの伝承や史実から、ギリシャ数学の誕生から原論の成立に至るまでを整理し、話をわかりやすくするために多少の創作を交えて短くまとめてみます。
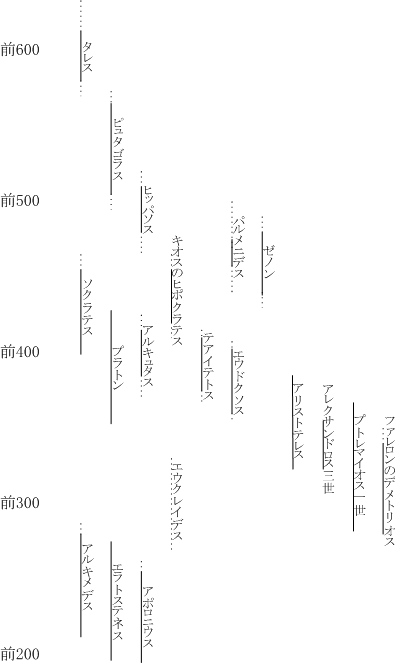
バビロニアやエジプトで発達した実用数学は、ギリシャに伝えられると証明という方法で洗練され、理論数学として独自の発展を遂げました。このギリシャ数学は前7世紀後半にフェニキア出身のタレスによって創始され、ピュタゴラス派によって継承されました。ヒッパソスを始めとするマテーマティコイと呼ばれる一派により神秘性の要素が加えられ、実用的な技術から自然哲学へと変容していきました。
前5世紀後半、ソクラテスの時代になると幾何学は広く大衆に普及していきます。前414年にアテナイで上演されたアリストファネスの人気喜劇『鳥』に「円の正方化」を実演する測量士が登場するほどでした。この頃にキオスのヒポクラテスが『原論』と題されたの最初の書を出版したと伝えられています。これはユークリッドの『原論』の最初の三巻に相当するものであったといわれています。
ソクラテスの弟子であったプラトンは、第一回イタリア・シケリア旅行の後の前387年にアテナイ郊外の神域であるアカデメイアに学園を創設しました。イタリアではピュタゴラス派の数学者・政治家であるタラスのアルキュタスに会い、大きな影響を受けました。後の著作『国家』にあるようにアカデメイアのカリキュラムでは哲学を学ぶための基礎科目として数学を重要視しました。アカデメイアの門には「幾何学を学ばざる者、入るべからず」という言葉が刻まれていたと伝えられています。アカデメイアにおける数学研究の中心となったのがテアイテトスとエウドクソスです。『原論』の第V巻以降のほとんどはこの二人の天才による業績であると考えられています。
前347年にプラトンが亡くなった後、アカデメイアの学頭は甥のスペウシッポスが継ぐことになります。アカデメイアで20年間学び、その後教師として学生の指導にあたっていたアリストテレスは出身地であるマケドニアに戻り、マケドニア王フィリッポス二世の王子アレクサンドロスの家庭教師になりました。このとき、後のプトレマイオス一世も一緒に学んでいます。この頃、アテナイはマケドニアと対立していましたが、前338年にカイロネイアの戦いでフィリッポス二世に屈服し、その子アレクサンドロス三世の時代には帝国に編入されました。前335年アレクサンドロス三世が即位するとアリストテレスはマケドニア支配下のアテナイに戻り、自らの学園リュケイオンを創設します。
前332年アレクサンドロス三世は、ナイル川河口にあるファロス島対岸で野営し、この地に海港としての利があることを悟り、ここに海港都市を建設することを決断し、当時最も前衛的といわれていた天才建築家ディノクラテスを招聘し、新都市アレクサンドリアの設計を担当させました。前323年にアレクサンドロス三世が急死すると、帝国は有力諸将により分割統治され、エジプトはプトレマイオスが支配することになりました。当初、地方総督として統治していたプトレマイオスは、アレクサンドロス一族の血が絶えた前306年にこのアレクサンドリアでプトレマイオス一世として王位につきました。
同時期にマケドニアはカッサンドロスとアンティゴノスがしのぎを削っていました。カッサンドロスはプトレマイオス・リュシマコス・セレウコスらと同盟を組んで対抗していました。カッサンドロスの右腕であり、アテナイのリュケイオン出身のファレロンのデメトリオスは前317年から10年間アテナイを統治していましたが、クーデターにより失脚し、前304年にプトレマイオス一世の招きでアレクサンドリアに移り、王の顧問となって国作りを助けました。
アレクサンドリア図書館とムーセイオンと呼ばれる学術研究所の創設はデメトリオスの進言によるものと考えられています。同じ師であるアリストテレスに学んだプトレマイオスですから、その戦略的意義を十分に理解していたことでしょう。そしてこの仕事には、アテナイで最高の学問を修め、政治家としての手腕も発揮していたデメトリオスが必要でした。
エウクレイデスの生涯についてはほとんどわかっていませんが、前330年頃エジプトに生まれ、アカデメイアで数学を学んだと考えられています。テアイテトスもエウドクソスもいないアカデメイアで主力級の数学者となり、デメトリオスがアテネイを統治していた時のつてでムーセイオンに招聘され、弟子とともに移りました。地理学者ストラボンによれば、ムーセイオンは王宮の一部で、散歩道、アーケードと会員専用食堂を備えていました。ムーセイオン会員は食住保証、納税免除、高額報酬という特別待遇で扱われていました。エウクレイデスはこの恵まれた環境で、ギリシャ数学の最高峰に達していたアカデメイアの数学を体系化する『原論』の編纂を始めました。その時期はムーセイオンが創設された前295年頃と考えられます。直接的な証拠はありませんが、この時期を境にして数学研究の中心がアテナイからアレクサンドリアに移っていることから、概ねこのような事情であったと考えられます。
イスラム教神学者のアル・ガッザーリ1058-1111が晩年、自らの思想遍歴をつづった『誤りからの救い』においてギリシャ哲学について次のように述べています。
「アリストテレスは形而上学の論理を体系づけ、その学問を組織立てた人で、不正確であったソクラテスやプラトンの理論を確実なものにし、未熟であった彼らの学問を完成したのである。」
この解釈は中世スコラ哲学にも影響を与え、アリストテレスは「万学の祖」と称されました。しかし、近代科学を学び、なおかつプラトンの著作を丹念に読んだ方であればこれには違和感を感じることでしょう。生涯、自分の考えを書物に著わすことをしなかったソクラテスは『パイドロス』において、文字が誕生したいきさつについてのエジプト神話を語ります。文字を発明した神タウトが王アンモンに
「王様、この文字というものを学べば、エジプト人たちの知恵は高まり、もの覚えはよくなるでしょう。私の発見したのは、記憶と知恵の秘訣なのですから。」
と言うと、王は反論します。
「たぐいなき技術の主テウトよ。技術上の事柄を生み出す力をもった人と、生み出された技術がそれを使う人々にどのような害をあたえ、どのような益をもたらすかを判別する人とは、別の者なのだ。…(中略)…あなたがこれを学ぶ人たちに与える知恵というのは、知恵の外見であって、真実の知恵ではない。すなわち、彼らはあなたのおかげで、親しく教えを受けなくてももの知りになるため、多くの場合ほんとうは何も知らないでいながら、見かけだけはひじょうな博識家であると思われるようになるだろうし、また知者となる代わりに知者であるといううぬぼれだけが発達するため、つき合いにくい人間となるであろう。」
この話は弟子のプラトンの著作によって現代の我々でも知ることができるわけですが、プラトンは人と人との対話という形式だけに限って書物として残しています。そして有名な第七書簡において、本当に大切なことは文字には書けないし、書くことはないと述べ、教える者と学ぶ者が生活を共にしながら、口承によって伝えていくしかないのだと言い切っています。
一方、アリストテレスは文字や書物という情報技術に異常なまでに執着します。自ら550巻ともいわれる著作を残しただけでなく、大量の書籍を収集しています。彼の教え子であったアレクサンドロスやプトレマイオス、デメトリオスに共通する情報戦略は、あきらかにアリストテレスの影響を受けています。しかし、アレクサンドリアがその後辿った悲劇的な歴史を考えれば、このような情報覇権主義が必ずしも成功するとは限らないことがわかります。それはやはり王アンモンがいうように、文字は知恵の外見であって、真実の知恵ではないからなのでしょうか。
最新の情報技術をどう利用するのか、どのような情報戦略をとればいいのかという問題には時代を超えた普遍性があり、口承文化と文字文化の対立の構図は現代においてもまったく同様です。GoogleやWikipediaに子供たちの教育を任せてしまっていいのかと考える親や教師は少なくないと思われます。
私はどちらに与する者でもなく、両方のバランスが大切だと考えていますが、しいて言えばプラトンの立場に近いでしょうか。
原論を読むこと自体は、豊富な日本語訳、英訳が用意されているのでそう難しいことではないように思えます。特に原論の最初の数巻についてはすでによく知っている初等幾何が題材となっているので、文章の意味がよくわからなくても、図を見ればだいたい意味がわかってしまいます。ときどき、文章がややおかしいとか、証明の手順がおかしいというようなことを感じるぐらいでしょう。ところが、第V巻に入ると突然世界が変わってきます。比や比例について語っているこの巻では、文章を読んでも、それが何を言わんとしているのかがわかりません。その文の文法的構造や単語の意味をすべて調べても意味が理解できないわけですから、途方に暮れてしまいます。
原論はエウクレイデスがアカデメイアの口承文化で体得した数学を、
整理・体系化し、アレクサンドリアの経済力や情報技術を利用して出版した書物であると考えられます。学生に教えるときには講義や演習の副読本として使われたことでしょう。この本は単に古代ギリシャ語を翻訳するだけでは読むことができません。口承で伝えられてきたマテーマティコイ語を解読する作業が要求されます。本居宣長が『古事記伝』で、古代の日本語は「意」(ココロ)と「事」(コト)と「言」(コトバ)がよく釣り合っていたと述べていますが、原論の文章はまさにそのとおりのもので、何の飾りも誇張も無く本質だけがそのまま言葉にされています。
私自身は第VI巻までの内容を、本書の第I部第1章に相当することを自分の頭で考えることによって、だいたい理解することができました。おもに休日を利用した作業で3年ぐらいかかっています。もっとも正確に理解できているかどうかは定かではありません。もしこれがアリストテレスによって書かれたものであればすぐに投げ出していたことでしょう。マテーマティコイの先達、テアイテトス、エウドクソスそしてエウクレイデスらが描いた体系は、本質を見極めた者にしか書けないものです。それは古代ギリシャ語を知らない人間がさまざまな訳を通して読んだとしてもわかります。
その後、第X巻は量的にやや多いことから、証明を飛ばして結果だけを一覧し、第XI巻と第XII巻の立体幾何の主要な結果をざっと読んでみましたが、同高同底の四面体が等積であることの取尽し法による証明では、精密な空間認識能力が要求され、こういうことはあまり経験が無いので頭が混乱しそうになりました。立体幾何について考えるときには、平面幾何のように紙と鉛筆だけではうまく絵が書けないために、頭の中で空間的イメージを組み立てることが必要なため、理解できるまでに時間がかかります。そして、そもそも立体幾何をきちんと学んだ経験が無いのでなおさらです。
このため第XI巻以降を正確に理解するには、現状のスキルや装備ではやや心もとないので、事前に立体幾何を現代的な手法で学んでおいて、さらにコンピュータグラフィックスで立体幾何の絵を描くためのツールを用意して、それから挑戦するという手順が無難だろうと考えました。
アカデメイアには空間認識能力を訓練する何らかの方法があったのでしょう。これがどのようなものであったかはわかりませんが、現代においてはコンピュータグラフィックスという格好の教材があります。これが原論を読むため、そしてコンピュータグラフィックスを学ぶための基礎としての第II部、第III部の発想です。
原論は山に喩えれば、昔は修験者のための修行の山であったものが、今は廃れ、草がぼうぼうで道がはっきりせず、足場が悪く、急な岩場も数多いという初心者が軽装備で登るには危険な山になってしまったようなものです。
本書は、まず原論の平面幾何の意味を翻訳する第I部「幾何学の基礎」から始まります。これは一言でいえば原論の文章を集合論や代数系の概念を使って書き換える試みです。エウクレイデスの時代にはまだ代数記号が発達していなかったために代数式が言葉で表現されています。これを元の文章の意味を変えないように記号化して表現するという作業を行いました。これでかなり見通しがよくなりました。
注意しなければならないのは、エウクレイデスは量について語っているということです。学校で教わるように、長さや面積が数であるとして読むのは誤りです。エウクレイデスが数と呼んでいるのは自然数だけで、実数は量の比としてしか考えていません。第I部「幾何学の基礎」は、原論を量の理論として読むためのガイドブックでもあります。この場合、原論と現代の初等幾何学との関係はどうなるのかという疑問が出てくるでしょう。これについては量の単位を定めて測定すると量比すなわち実数になると考えます。これにより学校教育のスキルをそのまま活かすことができるようになります。
第I部は原論を現代的な言葉で書き直すことを目標にしていますが、現段階では重要と思われる部分については厳密に記述してあるものの、それ以外の部分については覚書程度しか書いてありません。そのため体系としては不完全です。将来機会があれば、全体を見直した上で、本書とは別に最初から書き直してみようと考えています。
第I部では原論の5合目付近まで登り、そこから一旦下り、エルランゲンプログラムの丘を目指します。この丘で古典幾何の全体像を群論的視点から見渡します。最初から頂上を目指さずに第II部「平面幾何」コースでは低い位置をトラバースしながら古典幾何の峰々を一望します。そして最後にやや高い位置にある第III部「立体幾何」コースに螺旋状に登っていき、古典幾何の峰々を再び一望し、平面幾何と立体幾何の共通点と違いとを体感してから下山します。
単位と測定の原理を踏まえれば、第II部、第III部は、第I部とは独立して利用することができます。必要に応じて第I部を参照すれば、高校生や専門学校生がコンピュータグラフィックスを学ぶための「CGのための古典幾何学入門」として利用することも可能です。
本書では全体を通して、数とは比例であり、比例とは相似変換のことであるという一貫した立場をとっています。この立場からすると各部に次のような意味付けができます。
| 第I部 | 直線比例論 ⇔ 実数論 |
| 第II部 | 平面比例論 ⇔ 複素数論 |
| 第III部 | 空間比例論 ⇔ 四元数論 |
古典幾何学を比例論として見る視点は、ウィトルーウィウスの『建築書』にあるように比例は建築の一部であると考える建築家、遠近法や人体比例を研究したルネサンス期の画家・工芸家の考え方に近く、現代の職人達にも受け入れられやすいものでしょう。この立場でデューラーの『測定法教則』の現代版を書くというのは魅力ある題材です。
本書の続巻は、古典幾何学を応用したコンピュータグラフィックスの技法を解説するものになります。『測定法教則』に匹敵するようなものは書けませんが、教材用のCGツールを使いこなすためのマニュアルのようなものを考えています。
原論の頂上を目指すための書はこの続巻の後になります。時期的な見通しは立っていませんが、続巻で公開されるCGツールによって読者は立体図形を体感しながら読めるようになっているはずです。これにより原論の頂上に立つことができれば、すぐ近くにアルキメデスやアポロニウスの峰があり、そしてやや遠方には幻の名峰『プリンキピア』が見えることでしょう。ひょっとしたらその頂上へ到達できるルートが見えてくるかもしれません。
[2] アルパッド・サボー, ギリシア数学の始原, 玉川大学出版部, 1978
[3] 伊東 俊太郎, 数学の歴史(I) ギリシャの数学, 共立出版, 1979
[4] 中村 幸四郎, ユークリッド―原論の背景 (玉川選書), 玉川大学出版部, 1978
[11] 藤本 勝次, 筑摩世界文学大系(9) インド・アラビア・ペルシア集, 筑摩書房, 1977
[16] 粟野 頼之祐, ファレロンのデメトリオスとアレクサンドリア學府の創建について, 西洋古典學研究, 1954-06
人 物
エウクレイデス Euclidesユークリッド Euclid
ヒルベルト David Hilbert, 1862-1943
代表的著作『幾何学基礎論』において『原論』の平面幾何を公理論的に再構築しようと試みた。
アル・ガッザーリ 1058-1111イラン出身。イスラム教神学者。
Published by SANENSYA Co.,Ltd.