7.1節 線形Lie群
著者:梅谷 武
語句:対称群, 行列式, 正則行列, 一般線形群, 特殊線形群, 直交群, 特殊直交群, ユニタリ群, 特殊ユニタリ群, 線形Lie群
一般の線形空間並びに行列空間の内積・ノルム・行列式を定義する。さらに主要な線形Lie群について述べる。
作成:2009-09-23
更新:2021-03-28
ここでは、体Kが実数ℝあるいは複素数ℂであるときK上の線形空間について共通することについて述べます。
体
K上の線形空間
Vについて、写像
V × V  K,
(a,b) K,
(a,b)  〈 a,b 〉 〈 a,b 〉
|
が準双線形(双線形)かつ
エルミートえるみーと, Hermitian(対称)、正値であるとき、すなわち、次が成り立つとき、これを
内積ないせき, inner productという。ただし、実数のときは共役は恒等写像と考え、用語は括弧内にものに置き換える。
| (IN1)
| 〈 a + b, c 〉 = 〈 a, c 〉 + 〈 b, c 〉,
a,b,c ∈ V
|
| (IN2)
| λ 〈 a, b 〉 = 〈 λ a, b 〉,
a,b ∈ V, λ ∈ K
|
| (IN3)
| 〈 a, b 〉 = 〈 b, a 〉,
a,b ∈ V
|
| (IN4)
| 〈 a, a 〉 ≧ 0,
a ∈ V
|
| (IN5)
| 〈 a, a 〉 = 0 ⇔ a = 0
|
内積が定義された線形空間においてノルムを
によって定義します。
内積が定義された
K上の線形空間
V上のノルムは次の性質を満たす。
| (N1)
| a ≧ 0,
a ∈ V |
| (N2)
| a = 0 ⇔
a = 0 |
| (N3)
| λ a = λ a,
a ∈ V, λ ∈ K |
| (N4)
| 〈 a, b 〉 ≦
a b, a,b ∈ V |
| (N5)
| a + b ≦ a + b,
a,b ∈ V |
証明
略■
Knを
K上の
n次元線形空間と考えたとき、その二つの元
a,bの内積を
により、ノルムを
によって定義します。
上の定義は
K上の
n次元線形空間
Knの内積とノルムとしての性質を満たす。
証明
略■
ここでは、K上の(n,n)行列のなす行列環M(n,K)について考えます。
証明
略■
証明
略■
証明
略■
行列環
M(n,K)を線形空間と考えて、内積とノルムを次のように定義します。
K = ℝの場合、このノルムは第3章で定義した行列のノルムに一致します。
上の定義は行列環
M(n,K)を
K上の
n2次元線形空間と考えたときの内積とノルムとしての性質を満たし、さらに行列の積に関して次が成り立つ。
証明
略■
n個の
置換ちかん, permutationとは、
n個の数
{1,2,⋯,n}の並べ替え
| σ =
| 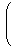 | | 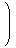 |
|
のことです。上段と下段は並べ替えの前と後に対応します。これは全単射
σ:{1,2,⋯,n}  {1,2,⋯,n},
i {1,2,⋯,n},
i  σ(i) σ(i)
|
と同じもので、
n個の置換全体の集合は写像の合成に関して群をなし、これを
対称群たいしょうぐん, symmetric groupSnといいます。
(n,n)行列
A = (aij) ∈ M(n,K)について、その
行列式ぎょうれつしき, determinantdet Aを
| det A := |
∑
σ ∈ Sn | | sgn(σ) x1σ(1) x2σ(2) ⋯ xnσ(n) |
|
|
|
によって定義します。
行列式に関して次が成り立つ。
| (7.20) | | det tA = det A, A ∈ M(n,K)
|
|
| (7.21) | | det (AB) = det A det B, A,B ∈ M(n,K)
|
|
証明
略■
行列
A = (aij) ∈ M(n,K)を
n個の
Knの直積の元と考えることができます。
| A =
| 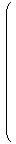 | | 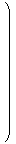 |
= (a1,a2,⋯,an)
|
このとき、行列式は
n個の
Knの直積上の関数と考えることができます。
det : Kn × ⋯ × Kn  K,
(a1,a2,⋯,an) K,
(a1,a2,⋯,an)  det (a1,a2,⋯,an)
det (a1,a2,⋯,an)
|
行列式は多重線形交代形式である。すなわち、次が成り立つ。
| (7.22) | | det(a1,⋯,aj + bj,⋯,an) =
det(a1,⋯,aj,⋯,an)
+ det(a1,⋯,bj,⋯,an)
|
|
| (7.23) | | det(a1,⋯,λ aj,⋯,an)
= λ det(a1,⋯,aj,⋯,an)
|
|
| (7.24) | | det(a1,⋯,ai,⋯,aj,⋯,an) =
- det(a1,⋯,aj,⋯,ai,⋯,an)
|
|
証明
略■
行列式はKnの元の列の線形独立性の判定に使うことができます。
Knの
n個の元について次が成り立つ。
| det(a1,a2,⋯,an) ≠ 0 ⇔
(a1,a2,⋯,an)が線形独立
|
証明
略■
一般に行列は線形写像と考えることができ、
(n,n)行列は
n次元線形空間における線形変換と考えることができます。行列式が
0でない行列は、基底となる
n個の元の列を線形独立な
n個の元の列に写すので線形同型写像を引き起こします。したがって、その逆変換を引き起こす
逆行列ぎゃくぎょうれつ, inverse matrixが存在します。これは
正則行列せいそくぎょうれつ, regular matrixと呼ばれます。正則行列全体のなす群は
一般線形群いっぱんせんけいぐん, general linear groupと呼ばれます。
| GL(n,ℝ) := { A ∈ M(n,ℝ) ∣ det A ≠ 0 }
|
は
実一般線形群じついっぱんせんけいぐん,
real general linear groupと呼ばれ、
| GL(n,ℂ) := { A ∈ M(n,ℂ) ∣ det A ≠ 0 }
|
は
複素一般線形群ふくそいっぱんせんけいぐん,
complex general linear groupと呼ばれます。これらは行列のノルムが定める距離によって、位相群(さらにはLie群)になっています。
Kn上に内積とノルムが定義されたことによって、Knを形式的に幾何学的空間のように扱うことができるようになります。平面や空間における合同変換は、内積とノルムを保存する線形変換として特徴付けられましたが、Knにおいても内積とノルムを保存する線形変換を定義することができます。
Kn上の内積において、次が成り立つ。
| (7.25) | | 〈 Ax, y 〉 = 〈 x, A†y 〉,
a,b ∈ Kn, A ∈ M(n,K)
|
|
証明
略■
A = (a1,a2,⋯,an) ∈ M(n,K)について、次は同値である。
| (a)
| AA† = En |
| (b)
| 〈 Ax, Ay 〉 = 〈 x, y 〉,
a,b ∈ Kn |
| (c)
| Ax = x, x ∈ Kn |
| (d)
| (a1,a2,⋯,an)はKnの正規直交基底である。
|
証明
略■
O(n),U(n),SL(n,ℝ),SL(n,ℂ),SO(n),SU(n)は線形Lie群である。
証明
略■
[
2] 横田 一郎,
群と位相, 裳華房, 1971
[
4] 江沢 洋, 島 和久,
群と表現, 岩波書店, 2009
数 学
エルミート えるみーと, Hermitian
内積 ないせき, inner product
跡 せき, trace
転置行列 てんちぎょうれつ, transpose matrix
随伴行列 ずいはんぎょうれつ, adjoint matrix
置換 ちかん, permutation
対称群 たいしょうぐん, symmetric group
互換 ごかん, transposition
偶置換 ぐうちかん, even permutation
奇置換 きちかん, odd permutation
符号 ふごう, signature
行列式 ぎょうれつしき, determinant
逆行列 ぎゃくぎょうれつ, inverse matrix
正則行列 せいそくぎょうれつ, regular matrix
一般線形群 いっぱんせんけいぐん, general linear group
実一般線形群 じついっぱんせんけいぐん,
real general linear group
複素一般線形群 ふくそいっぱんせんけいぐん,
complex general linear group
直交行列 ちょっこうぎょうれつ, orthogonal matrix
直交群 ちょっこうぐん, orthogonal group
ユニタリ行列 ゆにたりぎょうれつ, unitary matrix
ユニタリ群 ゆにたりぐん, unitary group
特殊線形群 とくしゅせんけいぐん, special linear group
実特殊線形群 じつとくしゅせんけいぐん, real special linear group
複素特殊線形群 ふくそとくしゅせんけいぐん, complex special linear group
特殊直交群 とくしゅちょっこうぐん, special orthogonal group
特殊ユニタリ群 とくしゅゆにたりぐん, special unitary group
線形Lie群 せんけいりーぐん, linear Lie group



