1.9節 面積論
著者:梅谷 武
語句:合同等積, 分割等積, 補充等積, テンソル積, 対称テンソル積, 交代テンソル積, 正方化, 二乗比, 極限等積
平面図形の等積性について論じ、面積量が対称テンソル積としての代数構造をもつことを示す。
作成:2009-08-27
更新:2011-03-08
線分の等積性と順序は二つの公理
| 公理2
| 重ね合わせることができるものは互いに等しい。
|
| 公理3
| 全体は部分より大きい。
|
によって完全に記述することができましたが、広がりのある平面図形の等積性はこれだけではうまく定義できません。これから定義するさまざまな等積性を区別するために、この公理2による等積性を
合同等積ごうどうとうせきと呼ぶことにしましょう。
農耕文明が要求する土地の等積性とは、形が等しいかどうかではなく、その土地にどれだけの作物が植えられるかということの基準を与えるものです。このことから自然に分割等積の概念が発生してきたものと考えられます。
二つの直線図形が
分割等積ぶんかつとうせきであるとは、それらを適当に直線図形に分割すると、それぞれで分割した図形の集合が一対一に対応し、なおかつ対応する図形どうしが合同等積であるようにすることができることである。
原論は議論の前提として、次の定理を暗黙裡に仮定しています。
すべての直線図形は互いの共通部分が頂点と辺のみの三角形に分割することができる。
証明
略■
ここでいう直線図形とは有限個の頂点と辺に囲まれたもので、分割された三角形の数も有限個です。原論の等積性に関する議論では補充等積というさらに弱い性質を使っています。
二つの直線図形が
補充等積ほじゅうとうせきであるとは、それらが合同な直線図形から合同な直線図形を引いたものあるいは加えたものに等しいことをいう。さらにこの定義において補充する図形の等積性を補充等積にしたもの、あるいは分割等積における分割図形の等積性を補充等積にしたものも補充等積であるという。
定義から合同等積ならば分割等積であり、分割等積ならば補充等積であることがわかります。
Area = {平面上の広がりをもつ直線図形全体}とし、Areaに属する二つの直線図形の面積が等しい、すなわち等積であるということを、それらが補充等積であることと定義します。この関係∼は同値関係であり、これによる商集合A+ := Area/∼を面積という量の集合と考え、これを面積量と呼ぶことにしましょう。線長量L+と同じように、任意の広がりをもつ直線図形に対して、その等積類を対応させる写像Area → A+が定まります。
第I巻は次のような順で面積論を展開していきます。
すべての三角形は指定角の平行四辺形に等積変形できる。
すべての直線図形は指定辺、指定角の平行四辺形に等積変形できる。
これらの結果を使って、すべての直線図形の面積を等積な長方形に還元して考えようというのが第II巻の基本的な発想になっています。
第II巻の冒頭にある定義II-1「すべての直角平行四辺形は直角を囲む二直線に囲まれているといわれる。」は、これだけですと何がいいたいのかよくわかりませんが、第II巻を通して読んでみると、結局これが原論における面積概念の本質を表現していることがわかってきます。
このことをこれまで準備してきた概念と記号によって表現してみましょう。
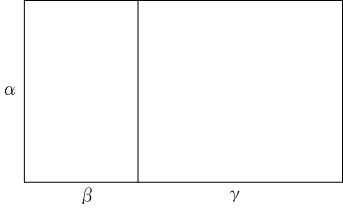
a ⊗E bで直角を挟む二辺の長さがそれぞれ
a,bであるような直角平行四辺形、すなわち長方形の等積類を表すものとします。
| L+ ⊗E L+ := { a ⊗E b | a,b ∈ L+ }
|
とおくと写像
L+ × L+  L+ ⊗E L+,
(a,b) L+ ⊗E L+,
(a,b)  a ⊗E b a ⊗E b
|
が定まります。第I巻の議論から
L+ ⊗E L+は面積量
A+と同じものであることがわかっていますので、
として議論を進めていきます。
このL+ ⊗E L+を原論の量体系に組み込むためには、これが可差半加群となることを示す必要があります。まず最初に加法を定義しましょう。
命題I-45より、
a ⊗E b, c ⊗E d, a,b,c,d ∈ L+とするとき、適当に
α ∈ Lineを定めたときに、
β, γ ∈ Lineを、
となるようにとることができます。このとき、和を次のように定義します。
| a ⊗E b + c ⊗E d := [α] ⊗E [β + γ]
|
これが線分の代表元のとり方によらないこと、可換律と結合律を満たすことはすぐにわかります。したがって、
L+ ⊗E L+は半加群になります。可差性は上の記号をそのまま使って
| [α] ⊗E [β + γ] =
[α] ⊗E [β] + [α] ⊗E [γ]
|
となることから、アルキメデス的も長さに関するアルキメデス性からわかります。したがって、
A+ = L+ ⊗E L+は無向量です。
次に比例倍を定義しましょう。
a ⊗E b, a,b ∈ L+, λ ∈ RL+とするとき、
| λ ( a ⊗E b ) := λ a ⊗E b = a ⊗E λ b
|
と定義します。
λ a ⊗E b = a ⊗E λ bは命題I-43の補形が等しいことからわかります。
対称化することによって、A = L ⊗E LはRL上の線形空間となり、次の命題が成り立ちます。
A = L ⊗E Lは
RL上の線形空間であり、写像
L × L  L ⊗E L,
(a,b) L ⊗E L,
(a,b)  a ⊗E b a ⊗E b
|
は
RL-
双線形そうせんけい, bilinearかつ
対称たいしょう, symmetricである。すなわち、次が成り立つ。
| (1.1) | | ( a + b ) ⊗E c = a ⊗E c + b ⊗E c, a,b,c ∈ L
|
|
| (1.2) | | a ⊗E ( b + c ) = a ⊗E b + a ⊗E c, a,b,c ∈ L
|
|
| (1.3) | | λ ( a ⊗E b ) = λ a ⊗E b = a ⊗E λ b,
a,b ∈ L, λ ∈ RL
|
|
証明
略■
テンソル積は具体的には、直積集合
M × Nが生成する自由
K-加群を
| ( a + b, c ) - ( a, c ) - ( b, a ) |
| ( a, b + c ) - ( a, b ) - ( a, c ) |
| ( λ a, b ) - λ ( a, b ), λ ∈ K |
| ( a, λ b ) - λ ( a, b ), λ ∈ K |
という形の元が生成する部分加群で剰余したものとして構成されます。
M = Nであり、剰余する部分加群の生成元に
を加えたものが対称テンソル積で、
を加えたものが交代テンソル積です。
面積量Aは線長量Lの対称テンソル積として作られていることがわかります。
今後はA = L ⊗ Lと書くことにします。
命題II-14「与えられた直線図形と等しい正方形を作図すること。」から、任意の長方形
a ⊗ b ∈ L+ ⊗ L+について、
なる
c ∈ L+が一意的に存在することがわかりますが、これは順序集合としての同型写像
L+ ⊗ L+  L+,
a ⊗ b L+,
a ⊗ b  c := √a ⊗ b c := √a ⊗ b
|
を引き起こします。与えられた図形に等積な正方形を作図することを
正方化せいほうかと呼ぶことにします。平方根と同じ記号で表しますが比に関する平方根ではなく、面積量を正方化したときの一辺の長さである線長量を意味しています。
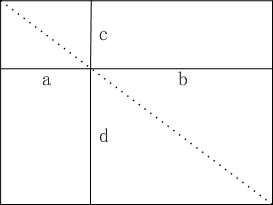
命題VI-17「三つの直線が比例するとき、その外項によって定まる長方形は中項によって定まる正方形に等積である。逆に外項によって定まる長方形が中項によって定まる正方形に等積であれば、三つの直線は比例する。」は、
| a ⊗ b = c ⊗ c ⇔ a:c ∝ c:b,
a,b,c ∈ L+
|
すなわち、長方形を正方化する問題が比例中項を求める問題と同等であることを意味しています。
命題VI-16「四つの直線が比例するとき、その外項によって定まる長方形は内項によって定まる長方形に等積である。逆に外項によって定まる長方形が内項によって定まる長方形に等積であれば、四つの直線は比例する。」は、
| a:b ∝ c:d ⇔ a ⊗ d = b ⊗ c,
a,b,c,d ∈ L+
|
と書き換えることができます。
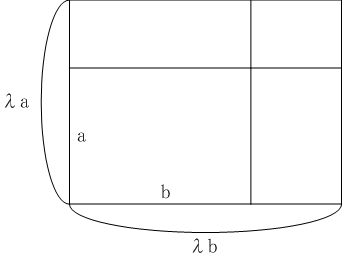
面積の比を求めるときに高さを固定すれば辺の比に一致することは上で見ましたが、今度は相似な図形、すなわち全体を同じ比率で拡大縮小したときの図形の比について考えます。
長方形の場合、
a,b ∈ L+, λ ∈ RL+のとき、
λ a ⊗ λ b = λ2 a ⊗ bより、
| a ⊗ b : λ a ⊗ λ b ∝ a : λ2 a
|
なります。このような状況を辺の比
λの
二乗比じじょうひをもっているといいます。
命題VI-19「相似な三角形の面積は対応する辺の比の二乗比をもつ。」と命題VI-20「相似な多角形は全体に比例する等しい数の相似な三角形に分割され、一方の多角形は他の多角形に対して、対応する辺の比の二乗比をもつ。」によって、相似な直線図形の面積の比が辺の比の二乗比をもっていることがわかります。
第II巻においては等積類を面積量と考え、正方化によってそれを測ろうとしていますが、この部分はかなり早い時期に成立していたと考えられます。第V巻においては、それまでの内容とは継続性がない抽象的な比例論が展開され、第VI巻においてこの比例論を応用して、高さを固定して底辺の比で比較することと、相似図形を二乗比で比較することについて議論されます。
第XII巻においては、取尽し法と呼ばれる、測りたい図形を直線図形の和として構成される図形でどんな指定量よりも小さい誤差で近似していく方法によって、円の面積がその直径上の正方形に比例することまで証明していますが、円を正方化することができませんでした。結局、1882年に
リンデマンLindemann, Carl Louis Ferdinand von, 1852-1939が円周率
πが超越的であることを証明し、与えられた図形に対して代数的な比をもつ図形しか作図できない原論の作図法では、円は正方化できないということがわかりました。
命題X-1「二つの等しくない量が与えられ、その大きい方からその半分より大きい量を引き、その残りからまたその半分より大きい量を引くという操作を限りなく繰り返すことができれば、小さい方の量より小さい量を残すことができる。」は無向量において0に限りなく近づく列を作る方法を与えるものです。
取尽し法は等積であることを示したい二つの図形に対して、それぞれに限りなく近づく列で、互いに補充等積であるようなものを構成することによって、その二つの図形が等積であると主張するものです。この意味の等積性を
極限等積きょくげんとうせきと呼ぶことにします。極限等積は補充等積よりさらに弱い等積性になっています。
このように古代ギリシアにおける面積概念は次のように段階的に発展していったと考えられます。
| 第1段階
| 正方化による方法
|
| 第2段階
| 比例論による方法
|
| 第3段階
| 取尽し法による方法
|
このうち比例論と取尽し法はエウドクソスの業績と考えられています。
1970年代後半に小島順先生が著わされた『線型代数』[
1]は当時の日本の数学界で論争を呼び、数学セミナー誌上で『線型代数を考える』[
2]という特集が組まれるほどでした。その後、小島先生は『量の計算を見直す』[
3]という連載において、学校教育における量の取り扱いの問題点を指摘し、量の概念をどのように理論化すればいいのかを詳細に論じました。その技法はまさにブルバキ流で読むのは大変ですが、抽象数学では言及されることのない「量」の概念を真正面からとらえようとした貴重な研究です。小島先生はこの量代数を理論として自立させるべきだと主張しましたが、30年の時を経てもその考えはあまり受け入れられていないようです。
この小島理論における面積概念を原論の体系に置き換えて再現し、原論における面積概念と比較してみましょう。
我々は線長量Lの"積"であるL ⊗ Lを二つの辺に囲まれる長方形の等積類という図形的な意味付けによって定義しました。小島理論においてはこれを意味付けしないでテンソル積として形式的に構成しています。ここでは意味を解釈しながら、その過程を見ていくことにします。
前節において線長量
L上の
RL-線形形式とは、単位
u ∈ Lを固定して、
さまざまな線分
a ∈ Lを測ること
u-1 : L  RL,
a = RL,
a = | | u  u-1(a) = u-1(a) = | |
|
であり、その線形形式全体のなす双対空間
L*上の
RL-線形形式とは、ある線分
a ∈ Lを固定して、さまざまな単位
u ∈ Lにより測ること
a : L*  RL,
u-1 RL,
u-1  u-1(a) = u-1(a) = | |
|
であることを見ました。
a,b ∈ Lについて、そのテンソル積
a ⊗ bを次のように定義します。
a ⊗ b : L* × L*  RL,
(u-1,v-1) RL,
(u-1,v-1)  u-1(a)v-1(b) = u-1(a)v-1(b) = | | |
|
これは
RL-双線形形式となります。この意味としては二辺
a,bを固定した
ときに、それらが囲む長方形をさまざまな単位の組
(u-1,v-1)で
測ることにあたります。
このときテンソル積
L ⊗ Lを次のように定義します。
| L ⊗ L := { L* × L*上のRL-双線形形式全体 }
|
L ⊗ Lは元のテンソル積全体の集合に一致し、写像
L × L  L ⊗ L
= { a ⊗ b | a,b ∈ L },
(a,b) L ⊗ L
= { a ⊗ b | a,b ∈ L },
(a,b)  a ⊗ b a ⊗ b
|
は
RL-双線形であり、
RL-線形空間としてのテンソル積になっている。
証明
略■
これは原論における面積とはかなり様子が異なっています。原論においては
a ⊗E bが二辺
a,bによって囲まれる長方形の等積類、すなわち面積という量そのものを意味していましたが、小島理論においてはテンソル積
a ⊗ bは長さの単位
u ∈ Lを定めたときに、双線形形式
a ⊗ b : L* × L*  RL,
(u-1,u-1) RL,
(u-1,u-1)  u-1(a)u-1(b) = u-1(a)u-1(b) = | | |
|
によって、その長方形に各辺の単位との比の積を対応させ、それを面積と考えています。いいかえれば、テンソル積
a ⊗ bは単位
uを定めたときに長方形をその面積である二辺の単位との比の積に対応させる測度関数を与えています。
このように同じ面積という概念を表現するために作られたものが、その意味を考えるとまったく異なった様相を示します。ところが、同じ一次元線形空間のテンソル積は対称であるため、テンソル積の普遍性から結局、双方はまったく同じ代数構造をもっていることがわかります。
面積量Aの等積類a ⊗ b ∈ A = L ⊗ Lに属する長方形の面積を測るとは、単位u ∈ L+を定めて、測定対象となる線分の組(a, b) ∈ L × Lとの比の組(a:u, b:u)を求めることです。線長量の場合と同様にこれをノルムとして表現します。
まず、線長量が単位uによって生成される一次元線形空間であることから、次がわかります。
面積量
A = L ⊗ Lは単位
u ∈ L+を定めると、
u ⊗ uから生成される線長比
RL上の一次元線形空間となる。
証明
略■
面積量上のノルムも比例倍を保存します。
面積量
Aのノルムについて次が成り立つ。
| (正値性)
| a ≧ 0かつa = 0 ⇔ a = 0, a ∈ A |
| (比例倍)
| λ a = λ a, λ ∈ RL,
a ∈ A |
| (三角不等式)
| a + b ≦ a + b, a,b ∈ A |
証明
略■
a ⊗ b ∈ L ⊗ Lを単位
u ∈ L+で表現すると、そのノルムを次のように表現できます。
したがって、ノルムを単位
u ∈ L+による各成分のノルムの積と定義するとノルムの性質を満たします。これを単位をもつ面積量のノルムと考えることにしましょう。
面積量
A = L ⊗ Lにおいて単位
u ∈ L+を定めるとき、そのノルムを単位
u ∈ L+による各成分のノルムの積と定める。
[
1] 小島 順, 線型代数, 日本放送出版協会, 1976
[
2] 小島 順, 齋藤 正彦, 森 毅, 特集/線型代数を考える, 数学セミナー, 1977-07
[
3] 小島 順, "量の計算"を見直す, 数学セミナー, 1977.8~1978.1
人 物
リンデマン Lindemann, Carl Louis Ferdinand von, 1852-1939
数 学
合同等積 ごうどうとうせき
分割等積 ぶんかつとうせき
補充等積 ほじゅうとうせき
双線形 そうせんけい, bilinear
対称 たいしょう, symmetric
テンソル積 てんそるせき, tensor product
対称テンソル積 たいしょうてんそるせき, symmetric tensor product
交代テンソル積 こうたいてんそるせき, alternating tensor product
正方化 せいほうか
二乗比 じじょうひ
極限等積 きょくげんとうせき